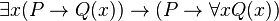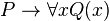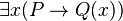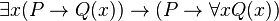Théorie des modèles - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La théorie des modèles est une branche de la logique mathématique. Son principe de base est qu’une théorie est mathématiquement valide si on peut définir un univers dans lequel elle est vraie.
Présentation de la théorie des modèles
Elle a été formulée d’une façon complète et cohérente d’abord par Alfred Tarski, dans un article fondateur, Le concept de vérité dans les langages formalisés, publié en 1933 (et traduit dans le recueil Logique, sémantique, métamathématique, Armand Colin 1972, pp.157-269). Tarski a considéré une formule apparemment triviale : "il neige" est une proposition vraie si et seulement s'il neige. (p.163). Il a compris que cette vérité élémentaire pouvait le conduire à apporter une réponse générale, puissante et satisfaisante au problème plusieurs fois millénaire de la nature de la vérité mathématique.
Tarski a appelé sa théorie la sémantique du calcul des prédicats, pour deux raisons :
- Elle donne une définition de la vérité et de la conséquence logique, indépendante de ce que donnent les démonstrations en logique.
- Elle donne une réponse partielle à la question de la signification du langage, parce que les mots ont du sens s'ils permettent de faire des phrases vraies dans un monde possible.
Mais ses racines sont beaucoup plus lointaines. Un premier modèle délibérément créé apparaît avec la naissance des géométries non euclidiennes. D'abord purement déductives, ces géométries ont peu à peu été acceptées à partir du moment où l'on a pu en donner des modèles, c'est-à-dire des supports géométriques avec des interprétations spécifiques pour désigner les droites. Poincaré par exemple donne un modèle du plan hyperbolique à partir d'un demi-plan du plan complexe.
Symétriquement, si l'on peut dire, l'abbé Buée et Jean-Robert Argand (plan d'Argand), puis ensuite Gauss et Cauchy donnent un modèle géométrique des nombres complexes.
Un modèle sert d'abord de structure pour valider une théorie logique ou mathématique.
Il existe deux notions de « consistance » ou de « cohérence » d'une théorie, a priori différentes, mais en fait équivalentes en logique classique du premier ordre, d'après le théorème de complétude de Gödel :
- un notion sémantique : une théorie est satisfaisable s'il existe un modèle dans lequel elle est vraie.
- une notion syntaxique : une théorie est non contradictoire si on ne peut en dériver à la fois une formule et sa négation.
Un système de déduction est dit « correct » (tous les systèmes usuels le sont) si l'existence d'un modèle donne la certitude de travailler sur une théorie qui ne débouchera pas sur une contradiction. L'intérêt est que pour montrer la cohérence ou consistance d'une théorie, il est souvent plus facile d'en déterminer un modèle que de montrer qu'on ne peut dériver de contradiction.
Le théorème de complétude de Gödel assure qu'en logique classique du premier ordre, la réciproque est vraie : toute théorie non contradictoire possède au moins un modèle. Il clôt des recherches qui remontent au théorème de Löwenheim (1915) et qui s’inspirent d’une approche hilbertienne de la vérité mathématique, et il fournit le fondement de la théorie des modèles.
Les modèles dans le calcul des prédicats
Dans le calcul des prédicats du premier ordre de la logique classique, les prédicats utilisés s'appliquent sur des variables. Pour définir un modèle, il convient donc d'introduire un ensemble dont les éléments serviront de valeurs à attribuer aux variables. Comme pour le calcul propositionnel, on commence par définir la vérité ou la fausseté des formules atomiques dans un domaine donné, avant de définir de proche en proche la vérité ou la fausseté des formules composées. On peut ainsi définir par étapes successives la vérité de toutes les formules complexes de la logique du premier ordre composées à partir des symboles fondamentaux d’une théorie.
Une formule est atomique lorsqu’elle ne contient pas d’opérateurs logiques (négation, conjonction, existentiation, ...). Atomique ne veut pas dire ici qu’une formule ne contient qu’un seul symbole mais seulement qu’elle contient un seul symbole de prédicat fondamental. Les autres noms qu’elle contient sont des noms d’objet et ils peuvent être très complexes. Qu’une formule est atomique veut dire qu’elle ne contient pas de sous-formule. Il s’agit d’une atomicité logique.
L'interprétation des formules atomiques dans un modèle
Une interprétation d'un langage du premier ordre est une structure, définie par les éléments suivants.
- Un ensemble U non vide, l’univers de la théorie. À chaque nom d’objet (constante) mentionné dans le langage est associé un élément de U.
- A chaque prédicat unaire (à une place) fondamental mentionné dans le langage est associé une partie de U, l’extension de ce prédicat. C'est l'ensemble des valeurs pour lequel on décide que le prédicat est vrai. À chaque prédicat binaire fondamental mentionné dans le langage est associé une partie du produit cartésien U × U, c’est l’ensemble de tous les couples pour lesquels le prédicat est vrai. De même pour les prédicats ternaires, ou d’arité supérieure.
- A chaque opérateur unaire mentionné dans le langage est associé une fonction de U dans U. À chaque opérateur binaire mentionné dans le langage est associé une fonction de U × U dans U. De même pour les opérateurs d’arité supérieure.
L’ensemble U, ou l’interprétation dont il fait partie, est un modèle d’une théorie lorsque tous les axiomes de cette théorie sont vrais relativement à cette interprétation.
L'usage du mot, modèle, est parfois multiple. Tantôt il désigne l'ensemble U, tantôt l'ensemble des formules atomiques vraies, tantôt l'interprétation. Souvent, quand on dit un modèle d'une théorie, on suppose automatiquement qu'elle y est vraie. Mais on dit aussi qu'une théorie est fausse dans un modèle.
La définition de la vérité des formules complexes
Dès qu’on a une interprétation d’une théorie, la vérité de toutes les formules qui mentionnent seulement les constantes, les prédicats et les opérateurs fondamentaux, peut être définie. On commence par les formules atomiques et on procède récursivement aux formules plus complexes.
On reprend les règles définies dans le paragraphe relatif aux modèles du calcul propositionnel, et on définit les deux règles supplémentaires, relatives au quantificateur universel et existentiel.
e)
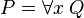
f)
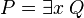
e) et f) permettent de définir la vérité et la fausseté de toutes les formules closes, c’est-à-dire sans variables libres.
La vérité et la fausseté de toutes les formules complexes, sans variables libres, de la logique du premier ordre, peut donc être déterminée dans un modèle donné.
Une formule vraie dans tout modèle s'appelle loi logique ou théorème. Comme pour le calcul propositionnel, le théorème de complétude de Gödel énonce l'équivalence entre loi logique et formule prouvable dans un système de déduction adéquat. Ce résultat est remarquable, compte tenu du fait que, contrairement au calcul des propositions, le nombre de modèles pouvant être envisagé est en général infini. D'ailleurs, contrairement au calcul des propositions, le calcul des prédicats n'est pas décidable.
Exemples
La formule
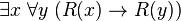
- Ou bien on attribue la valeur vraie à R(y) lorsque y se voit attribué une valeur quelconque dans U, et dans ce cas, on attribue à x une valeur quelconque dans U. L'implication
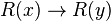
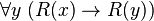
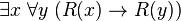
- Ou bien on attribue la valeur faux à R(y) pour au moins un y dans U. Désignons alors par x cet élément. Alors pour tout y de U,
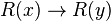
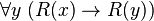
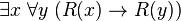
Dans les deux cas, la formule est vraie. U étant quelconque, la formule est vraie dans tout modèle, et peut également être prouvée au moyen d'un système de déduction.
Par contre, la formule