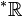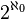Nombre hyperréel - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Introduction : pourquoi les hyperréels ? - Construction - Historique - Un exemple d'utilisation - Définitions

Introduction

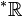
En mathématiques, les nombres hyperréels constituent une extension $^*\mathbb R$ des nombres réels usuels, permettant de donner un sens rigoureux aux notions de quantité infiniment petite ou infiniment grande ; techniquement, on utilise une ultra-puissance pour construire cette extension. On peut aussi définir les nombres hyperréels par le biais d'un modèle non-standard des nombres réels.

Introduction : pourquoi les hyperréels ?

Les « infiniments petits » de l'analyse du XVII^e siècle avaient suscité de violentes critiques, assez semblables à celles provoquées par l'introduction de « nombres imaginaires » de carré négatif. Les problèmes techniques correspondants ne purent cependant pas être résolus, ce qui amena la disparition progressive des infinitésimaux et leur remplacement, dû à Cauchy et Weierstrass, par les notions modernes de limite, de continuité, etc.

Cependant, on pouvait encore envisager d'adjoindre aux réels de nouveaux objets permettant de rendre rigoureux les raisonnements utilisant les infiniment petits, et diverses tentatives furent faites dans ce sens (par exemple par Hadamard et du Bois-Reymond), mais cela sans grand succès, pour des raisons que seule la logique mathématique devait rendre claires.

Les travaux de Skolem montraient cependant dès 1930 qu'une extension des réels, autorisant un véritable calcul infinitésimal, était néanmoins possible. Il existe d'ailleurs en réalité plusieurs de ces extensions, mais le choix exact de l'une d'entre elles n'a pas de grandes conséquences pratiques (bien qu'elles ne soient pas toutes isomorphes) ; on appelle en général « nombres hyperréels » l'une quelconque d'entre elles.

Un nombre hyperréel (non réel) pourra représenter ainsi, par exemple, une quantité « plus grande que tout entier » (donc "infiniment grande") ou « plus petite que l'inverse de tout entier » (donc infinitésimale), mais aussi un réel infiniment proche de 1, mais strictement plus petit que lui.

Construction

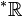
L'objectif est de construire un surcorps $^*\mathbb R$ de $\mathbb R$ possédant des nombres infiniment grands et infiniment petits. Ce surcorps devra rester totalement ordonné et vérifier que tout nombre x non infiniment grand s'écrit x*+ε avec x* un nombre réel et ε un nombre infinitésimal.

Cette construction fait assez naturellement intervenir des suites de nombres réels ; ainsi la suite $(1 / n)$ s'interprète comme un nombre infiniment petit et (n²) comme un infiniment grand. Les nombres réels sont préservés dans les suites constantes. L'addition et la multiplication des suites fournissent de bonnes bases pour obtenir une structure de corps. Malheureusement il manque l'ordre total : il n'est pas clair si le nombre hyperréel défini par la suite oscillante (1, -1, 1, -1, ...) est strictement positif ou strictement négatif. On observe cela dit qu'étant donné deux suites de réels, les ensembles d'indices où l'une est supérieure à l'autre sont complémentaires. 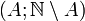Choisir un ordre total sur les nombres hyperréels est donc équivalent à choisir une partie de N dans chaque couple de parties $(A; \mathbb{N}\setminus A)$ . Ce dernier choix amène directement à la notion d'ultrafiltre sur N, de laquelle découle toute la construction qui suit.

La construction des hyperréels se fait à partir d'un ultrafiltre U sur N qui ne contient aucune partie finie de N (on dit que c'est un ultrafiltre libre). On ne peut malheureusement pas exhiber un tel ultrafiltre U, dont l'existence repose sur le raffinement du filtre des parties cofinies de N par le lemme de Zorn, et donc en définitive sur l'axiome du choix.

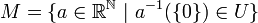
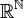
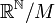
On construit l'ensemble M des suites de réels $(z n)$ dont l'ensemble des indices n où $z n = 0$ est un élément de l'ultrafiltre. On peut écrire de manière condensée $M = \{a \in \mathbb R^{\mathbb N}\ |\ a^{-1}(\{0\}) \in U\}$ . Un tel ensemble M est un idéal maximal de l'anneau commutatif des suites de réels $\mathbb R^{\mathbb N}$ . Donc l'anneau quotient $\mathbb R^{\mathbb N} / M$ est un corps ordonné commutatif qui contient $\mathbb R$ . Cet ensemble (muni des lois induites par le quotient) est un surcorps de $\mathbb R$ totalement ordonné. Il contient par exemple l'infiniment petit (1,1/2,1/3,...,1/n,...) (ou plus précisément la classe d'équivalence de cette suite). On perd par contre le théorème de la borne supérieure sur les nombres hyperréels.

On note que le cardinal de $^*\mathbb R$ est $2^{\aleph_0}$ et donc cet ensemble est équipotent à $\mathbb R$ ; cependant, on peut montrer que l'ensemble exact obtenu dépend de l'ultrafiltre choisi : tous les systèmes de nombres hyperréels construits ainsi ne sont pas isomorphes entre eux.