Théorie des ensembles - Définition

Introduction

La théorie des ensembles est une branche des mathématiques, créée par le mathématicien allemand Georg Cantor à la fin du XIX^e siècle.

La théorie des ensembles se donne comme primitives les notions d'ensemble et d'appartenance, à partir desquelles elle reconstruit les objets usuels des mathématiques : fonctions, relations, entiers naturels, relatifs, rationnels, nombres réels, complexes... C'est pourquoi la théorie des ensembles est considérée comme une théorie fondamentale dont Hilbert a pu dire qu'elle était un « paradis » créé par Cantor pour les mathématiciens.

En plus de proposer un fondement aux mathématiques, Cantor introduisait avec la théorie des ensembles des concepts radicalement nouveaux, et notamment l'idée qu'il existe plusieurs types d'infini que l'on peut mesurer et comparer au moyen de nouveaux nombres (ordinaux et cardinaux).

À cause de sa modernité, la théorie des ensembles fut âprement controversée, notamment parcequ'elle postulait l'existence d'ensembles infinis, en contradiction avec certains principes des mathématiques constructives ou intuitionnistes.

Au début du XXème siècle plusieurs facteurs ont poussé les mathématiciens à développer une axiomatique pour la théorie des ensembles : la découverte de paradoxes tels que le paradoxe de Russell, mais surtout le questionnement autour de l'hypothèse du continu qui nécessitait une définition précise de la notion d'ensemble. Cette approche formelle conduisit à plusieurs systèmes axiomatiques, le plus connu étant les , mais également la théorie des classes de von Neumann ou la théorie des types de Russell.

Les origines de la théorie des ensembles

Génèse

Cantor est le principal créateur de la théorie des ensembles qu'il a introduite au début des années 1880. C'est en travaillant sur des problèmes de convergence des séries trigonométriques, dans les années 1870, qu'il a été amené à définir une notion de dérivation des ensembles de nombres réels : étant donné un ensemble X de réels, son dérivé X' est X duquel on a supprimé tous les points isolés. Par exemple si on prend l'ensemble alors chaque nombre 1 / n est isolé dans X si bien que X' est simplement {0}. Ce dernier ensemble peut à son tour se dériver et son dérivé est l'ensemble vide.

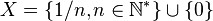
Si maintenant on prend alors chaque 1 / n + 1 / p est isolé dans Y si bien que le dérivé Y' est X. On voit donc que l'ensemble Y peut se dériver trois fois.

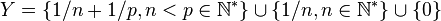
En itérant ce procédé on peut ainsi construire un ensemble X de réels qui se dérive une infinité de fois au sens suivant : si on note X⁽ⁿ⁾ le n-ième dérivé de X alors les X⁽ⁿ⁾ forment une suite décroissante (pour l'inclusion) d'ensembles ; le dérivé infini de X est l'intersection de tous les X⁽ⁿ⁾ que l'on note . Mais cela ne s'arrête pas là : Cantor a découvert l'existence d'ensembles de réels tels que contient des points isolés, donc est encore dérivable. Il y a ainsi des ensembles que l'on peut dériver une infinité + 1 fois, une infinité + 2 fois, ..., 2 infinités de fois, etc. Il semblait donc exister une arithmétique de l'infini et c'est en explicitant celle-ci que Cantor a développé la théorie des ensembles.

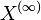
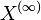
L'idée fondamentale a été de définir l'équipotence : deux ensembles A et B sont équipotents, ou ont même cardinalité (même nombre d'éléments quand ils sont finis), s'il existe un moyen d'associer à chaque élément de A un et un seul élément de B et inversement. On peut ainsi démontrer que l'ensemble des entiers naturels a la même cardinalité que l'ensemble des nombres rationnels, bien que soit un sous-ensemble propre de . Ces deux ensembles sont dits infinis dénombrables. D'un autre côté, l'ensemble des nombres réels n'a pas la même cardinalité que ou , mais une cardinalité supérieure que l'on appelle la puissance du continu. Cantor a donné deux preuves que n'est pas dénombrable, et la deuxième, qui utilise un argument connu sous le nom d'argument de la diagonale de Cantor, a été extraordinairement influente et a eu de nombreuses et diverses applications en logique et en mathématiques.

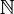
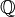
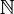
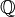
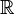
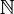
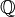
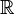
Cantor a approfondi la théorie et a construit des hiérarchies infinies d'ensembles infinis, les nombres ordinaux et les nombres cardinaux. Ces constructions étaient controversées à son époque, l'opposition étant conduite par le finitiste Léopold Kronecker ; mais aujourd'hui elles sont acceptées par la majorité des mathématiciens.

Et développement

La notion de cardinal d'un ensemble a conduit Cantor a poser une question qui devait devenir fondatrice : existe-il des ensembles de réels qui sont non dénombrables (ils ont strictement plus d'éléments que ) mais n'ont pas non plus la puissance du continu (ils ont strictement moins d'éléments que ) ? Cette question connue sous le nom de l'hypothèse du continu n'a pas obtenu de réponse du vivant de Cantor (il a fallu attendre Gödel en 1938 pour avoir une première demi-réponse) mais a suscité de nombreux travaux et notamment le développement de la théorie axiomatique des ensembles.

La théorie de Cantor est considérée comme « naïve » parcequ'elle n'emploie pas encore une axiomatique précise, et parce que pour lui il n'y avait qu'une seule théorie des ensembles, un seul univers ensembliste attendu, alors que les théoriciens des ensembles d'aujourd'hui jonglent avec des univers différents.

Après coup, on a pu simplifier, assez injustement pour Cantor, en résumant sa théorie à un usage tacite de l'axiome d'extensionnalité, et d'une version trop forte du schéma d'axiomes de compréhension, qui en substance permettrait d'associer à toute propriété l'ensemble des objets vérifiant cette propriété. Une telle théorie, que l'on n'attribuera pas à Cantor, est contradictoire. Elle mène à deux familles de paradoxes. Les uns, comme le paradoxe de Berry ou le paradoxe de Richard, se rattachent au fait que le langage n'est pas bien défini, les autres, comme le paradoxe de Russell à un usage trop large de la compréhension : quand on essaie de construire l'ensemble S = {A | A∉A} de tous les ensembles qui n'appartiennent pas à eux-mêmes on tombe sur une contradiction. L'actuel schéma d'axiomes de compréhension, proposé par Zermelo, est restreint afin d'éviter ce paradoxe.

Cantor connaissait, avant la découverte du paradoxe de Russell, des paradoxes plus complexes, mais de même nature, comme le paradoxe de Burali-Forti ou le paradoxe du plus grand cardinal. Beaucoup de théoriciens des ensembles s'entendent pour dire que l'axiomatisation la plus adéquate à la théorie développée par Cantor est la théorie ZFC avec axiome de fondation (voir ci-dessous), ou la théorie des classes de von Neumann, Gödel et Bernays, qui lui est, en un certain sens (qui peut être rendu précis), équivalente.

Au tournant du siècle, Cantor est de plus en plus handicapé par sa maladie nerveuse, mais ses solutions aux paradoxes circulent par sa correspondance et sont connues, à la fin du XIX^e siècle, de Richard Dedekind et, à Göttingen, de David Hilbert et de Ernst Zermelo. Cependant, pour beaucoup de mathématiciens de l'époque, les paradoxes jettent un doute sur la validité de la théorie des ensembles, les solutions proposées par Cantor sont trop informelles pour convaincre ceux qui les connaissent. Certains s'orientent vers la méthode axiomatique, illustrée à la même époque par Hilbert pour les fondements de la géométrie (1899).

Ainsi, en 1908, Ernst Zermelo construit un système d'axiomes pour la théorie des ensembles. En dehors de l'axiome d'extensionnalité, on peut voir ces axiomes comme une restriction de la version contradictoire du schéma d'axiomes de compréhension aux cas particuliers utiles, qui ne permettent pas de dériver les paradoxes. Dans ce système, il inclut également l'axiome du choix (qui n'a rien à voir avec la compréhension), un axiome à l'époque très controversé, avec lequel il a montré (en 1904) le théorème du bon ordre, et qui a également été utilisé implicitement par Cantor. Le système de Zermelo a été complété dans les années 1920 par Abraham Adolf Fraenkel et Thoralf Skolem, qui ajouteront le schéma d'axiomes de remplacement (autre cas particulier de la compréhension non restreinte), donnant la théorie connue aujourd'hui sous le nom de ZF (sans axiome du choix) ou ZFC (avec axiome du choix). D'autres auteurs ont depuis travaillé sur le problème de l'axiomatisation de la théorie des ensembles, notamment John von Neumann qui a défini une alternative très intéressante à ZF : la théorie des classes.