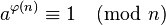Petit théorème de Fermat - Définition

Généralisations

Une légère généralisation du théorème, qui découle immédiatement de celui-ci, s'énonce de la manière suivante : si p est un nombre premier et si m et n sont des entiers strictement positifs tels que m ≡ n (mod p-1), alors pour tous entiers a, a^m ≡ aⁿ (mod p). Sous cette forme, le théorème est utilisé pour justifier l'algorithme de chiffrage RSA à clé publique.

Le petit théorème de Fermat est généralisé par le théorème d'Euler : pour tout entier naturel non nul n et tout entier a premier avec n, on a

où φ(n) désigne la fonction φ d'Euler comptant les entiers entre 1 et n qui sont premiers avec n. Si n est un nombre premier, alors φ(n) = n - 1, on retrouve le petit théorème de Fermat.

La démonstration se fonde sur le fait que le groupe des unités de l'anneau Z/nZ est d'ordre φ(n).