Petit théorème de Fermat - Définition
La liste des auteurs de cet article est disponible ici.
Exemples
Voici quelques exemples du théorème :
- 53 − 5 = 120 est divisible par 3
- 72 − 7 = 42 est divisible par 2.
- 25 − 2 = 30 est divisible par 5.
- (−3)7 + 3 = − 2 184 est divisible par 7.
- 297 − 2 = 158 456 325 028 528 675 187 087 900 670 est divisible par 97.
Démonstrations
Arithmétique modulaire

La connaissance de la structure et particulièrement du groupe des unités de l'anneau Z/pZ, permet une démonstration simple du théorème. Si p est un nombre premier, le groupe des unités Z/pZ* est un groupe cyclique d'ordre p - 1, donc isomorphe à Z/(p - 1)Z.
Une première approche consiste à considérer φ cet isomorphisme. L'image φ(ap-1) de ap-1 est égale à (p - 1)φ(a), correspondant à l'élément neutre du groupe. On en déduit que ap-1 est l'élément neutre de Z/pZ*, c'est-à-dire la classe de l'unité, ce qui termine la démonstration.
Une deuxième approche est l'application du théorème de Lagrange, l'ordre de tout élément d'un groupe fini est un diviseur de l'ordre du groupe. En conséquence, si θ est l'ordre de a, alors il existe un entier μ tel que θ.μ = p - 1. L'entier a θ est un élément de la classe de l'unité par définition de l'ordre d'un élément (cf le paragraphe Définitions de l'article Groupe cyclique) et donc a p - 1= a θ.μ est aussi élément de la classe de l'unité.
Ces approches correspondent à la fois au travail de Gauss et aux démonstrations modernes, ce sont en effet les plus concises.
Démonstration d'Euler et de Leibniz
Il existe une autre démonstration, utilisant la formule du binôme de Newton. Cette démonstration correspond à celle d'Euler et de Leibniz.
Elle utilise un raisonnement par récurrence sur la valeur a. Pour une raison de simplicité, les notations utilisées ici sont celles de Gauss, utilisant les congruences. Si ces notations ne correspondent pas à celles de l'époque, le raisonnement est néanmoins identique.
Avant de démontrer cette récurrence, un petit lemme est utile :
- Soient a et b deux entiers, alors (a + b)p est congru à ap + bp modulo p.
Il suffit de développer l'expression (a + b)p et de remarquer que tous les coefficients binomiaux à l'exception du premier et du dernier sont des multiples de p si p est premier. La démonstration est donnée dans le paragraphe Diviseurs et coefficients binomiaux de l'article Coefficient binomial.
- La proposition est vraie si a est égal à un.
En effet, 1p est bien congru à un modulo p.
- Supposons la proposition établie si a est égal à k et démontrons-la pour k + 1.
Une démonstration arithmétique élémentaire
Il existe également une autre démonstration qui utilise essentiellement le lemme d'Euclide, la division euclidienne et l'identité de Bézout.
-
- Si a n'est pas premier avec p, alors a p - a est un multiple de p.
D'après le lemme d'Euclide a est un multiple de p, il en est de même de a p et de a et donc de leur différence.
Pour la suite de la démonstration, a est supposé être premier avec p. Pour étudier ce cas, il est nécessaire d'établir un lemme :
Remarquons tout d'abord que p est premier avec a et k, le reste de la division de a.k par p n'est donc jamais égal à zéro et l'ensemble d'arrivé est bien celui de la fonction φ.
Montrons alors l'injectivité de φ. Soit k1 et k2 deux entiers de l'intervalle [1, p - 1], ayant même image par φ et tel que k1 est supérieur ou égal à k2. On remarque de p divise a.(k1 - k2). Comme p est premier avec a, il divise k1 - k2 d'après le lemme d'Euclide. Comme k1 - k2 est élément de l'intervalle [0, p - 1] et que p est premier, k1 est égal à k2.
La surjectivité de φ est une conséquence du fait que toute application injective d'un ensemble fini dans lui-même est surjective.
-
- Le reste de la division euclidienne de (p - 1)!a p-1 par p est égal au reste de la division euclidienne de (p - 1)! par p.
Ici, le symbole ! désigne l'application factorielle. Cette proposition utilise le fait que si r1 et r2 désignent les restes de la division euclidienne de deux entiers n1 et n2 par p, alors les produits n1.n2 et r1.rr ont même reste pour la division euclidienne par p. Cette propriété est étudiée dans l'article Congruence sur les entiers.
Une simple récurrence permet alors d'établir que la division euclidienne de (p - 1)! par p possède le même reste que la division euclidienne du produit des φ(k) si k parcourt l'intervalle [1, p - 1] d'après la proposition précédente. Elle montre aussi que le reste que la division euclidienne du produit des φ(k) si k parcourt l'intervalle [1, p - 1] par p est égal au reste de la division euclidienne de (p - 1)!a p-1 par p. Ce qui démontre la proposition.
-
- La valeur a p - a est un multiple de p.
Comme p est un nombre premier, le lemme d'Euclide montre qu'il est premier avec (p - 1)!, l'identité de Bézout montre l'existence de deux entiers m et n tel que :
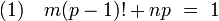
On en déduit que m.(p - 1)! possède pour reste de la division euclidienne par p, la valeur un. L'égalité (1) montre que :
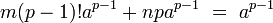
Le reste de la division euclidienne de a p-1 par p est donc égal à celui de la division euclidienne de m.(p - 1)!a p-1. La proposition précédente montre que ce reste est égal au reste de la division euclidinne de m.(p - 1)!, qui est égal à un. Ce qui montre que a p-1 - 1 est un multiple de p et une multiplication par a termine la démonstration.
Démonstration du corollaire du petit théorème de Fermat
1er cas Si a est divisible par p, alors ap - a est divisible par p
2ème cas Si a n'est pas divisible par p, alors, d'après le petit théorème de Fermat, ap-1 -1 est divisible par p. Donc (ap-1 -1) x a est divisible par p

















































