Anneau Z/nZ - Définition

Introduction

En mathématiques, et plus particulièrement en algèbre, Z/nZ est un cas particulier d'anneau, correspondant au calcul modulaire sur les restes des entiers dans la division par n.

Tout anneau unitaire contient soit un sous-anneau isomorphe à Z/nZ soit à Z l'anneau des entiers.

Cet anneau joue un rôle particulier en arithmétique, il est en effet l'outil de base de l'arithmétique modulaire.

L'article Congruence sur les entiers traite le même sujet avec une approche plus didactique et moins exhaustive, tandis que l'article Arithmétique modulaire traite de l'histoire de ce concept, des outils utilisés ainsi que de ses applications.

Construction de Z/nZ

Idéaux de Z

La division euclidienne dans Z montre que cet ensemble est un anneau euclidien, en conséquence Z est un anneau principal. Cela signifie que pour tout idéal I de Z, il existe un entier n tel que I est égal à nZ. Comme les idéaux nZ et -nZ sont confondus, il est toujours possible de choisir n positif. Dans toute la suite de l'article n désigne un entier positif.

Anneau quotient

La construction de Z/nZ correspond à la construction générale des anneaux quotients. Ici la relation d'équivalence correspond à la classique congruence sur les entiers. Un élément de Z/nZ est la classe des éléments ayant tous le même reste par la division euclidienne par n.

Un élément est identifié par un membre de sa classe, souvent l'entier compris entre 0 et n - 1. Il est parfois noté ou , ainsi dans Z/6Z, désigne la classe contenant les éléments 2, 8, 14 etc... Quand il n'existe pas d'ambigüité, on utilise simplement la lettre a.

• Les éléments de Z/nZ sont appelés classes modulo n ou résidu.

Groupe des unités

Le groupe des unités d'un anneau correspond au groupe multiplicatif formé des éléments inversibles. De tels éléments sont appelés unité.

• Soit m un entier, sa classe est une unité si et seulement si m est premier avec n.

Si m est premier avec n alors il est inversible, sinon soit d un diviseur commun différent de un, soit k l'entier tel que d.k = n, le fait que m.k soit un multiple de n montre que m est un diviseur de zéro et donc est non inversible.

• L'ordre du groupe des unités est égal à φ(n) si φ désigne la fonction indicatrice d'Euler.

Un élément du groupe additif Z/nZ est générateur si et seulement s'il est premier avec n, car son ordre est alors égal à n. Or le paragraphe Indicatrice d'Euler de l'article Groupe cyclique montre que le nombre d'éléments générateurs est égal à φ(n).

Cas où n est premier

Dans le cas où n est premier c'est-à-dire si l'anneau est un corps, la structure est la suivante :

• Si n est un nombre premier, le groupe des unités du corps Z/nZ est un groupe cyclique d'ordre n - 1.

En effet, tout élément autre que celui nul est inversible, l'ordre du groupe multiplicatif est donc n - 1. Le groupe multiplicatif est naturellement fini, il admet un exposant e, l'exposant est le plus petit commun multiple des ordres des différents éléments du groupe multiplicatif. Considérons le polynôme de Z/nZ[X] suivant : X^e - 1. Il admet pour racines tous les éléments du groupe multiplicatif donc n - 1 racines différentes. Or tout polynôme à coefficients dans un corps possède un degré supérieur ou égal à son nombre de racines. On en déduit que e est supérieur ou égal à n - 1. Le théorème de Lagrange, qui a pour corollaire le fait que l'ordre d'un élément est un diviseur de l'ordre du groupe, montre que e est égal à n - 1.

Pour conclure il suffit de constater que tout groupe abélien fini possède un élément d'ordre l'exposant, cette propriété est démontrée dans l'article détaillé. Le groupe multiplicatif possède un élément d'ordre le cardinal du groupe et qui est donc primitif, ce qui montre que le groupe est cyclique et termine la démonstration.

Remarque : un raisonnement de cette nature montre que tout groupe multiplicatif fini d'un corps commutatif est aussi cyclique.

Cas où n n'est pas premier

Dans le cas où n n'est pas premier, la structure est naturellement celle d'un groupe abélien fini elle correspond donc à un produit de groupes cycliques d'après le théorème de Kronecker. La structure est plus complexe que celle du cas précédent, plusieurs propositions sont nécessaires pour l'expliciter.

• Soit n et m deux entiers premiers entre eux, le groupe des unités de Z/n.mZ est isomorphe au produit direct des groupes des unités de Z/nZ et de Z/mZ.

C'est une conséquence du théorème chinois.

Le théorème fondamental de l'arithmétique limite alors l'étude au cas ou n est égal à p^r avec p un nombre premier et r un entier strictement positif. Deux configurations se présentent :

• Si p est égal à deux et r supérieur ou égal à trois, le groupe des unités est le produit direct d'un groupe d'ordre deux engendré par la classe de -1 et d'un groupe cyclique engendré par la classe de 5.

• Si p est différent de deux, alors le groupe des unités est cyclique.

Tous les cas ne sont pas traités, il reste celui ou p est égal à deux et r est égal à un ou deux. Cependant ces cas sont triviaux, le groupe contient un ou deux éléments et par conséquent est cyclique.

• Soit m un entier, sa classe est une unité si et seulement si m est premier avec n.

Si m n'est pas premier avec n, ils ont un diviseur a commun différent de 1 et de n. Soit b l'entier tel que a.b soit égal à n, alors la classe de m.b est la classe nulle donc les classes de m et de b sont des diviseurs de zéro.

Réciproquement si m est premier avec n, alors l'identité de Bézout montre l'existence d'un entier a tel que la classe de a.m est celle de l'unité, en conséquence m est une unité.

• L'ordre du groupe des unités est égal à φ(n) si φ désigne la fonction indicatrice d'Euler.

C'est une conséquence directe de la proposition précédente, φ(n) désigne exactement le nombre d'entier inférieur à n et premier avec n.

• Si p est égal à deux et r supérieur ou égal à trois, le groupe des unités est le produit direct d'un groupe d'ordre deux engendré par la classe de -1 et d'un groupe cyclique engendré par la classe de 5.

Pour démontrer cette proposition vérifions d'abord l'égalité suivante par récurrence sur k :

Pour k égal à 1, l'égalité est vrai avec λ égal à 3. Supposons le résultat vrai pour k et montrons le pour k + 1

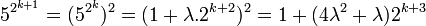
Il existe un morphisme ψ de groupe de Z/2^rZ^* dans Z/4Z^*.

L'anneau quotient de cardinal 2^r admet un idéal de cardinal 2^{r - 2} car le deuxième cardinal divise le premier. Le quotient de Z/2^rZ par Z/2^r-2Z est isomorphe à l'anneau Z/4Z. Soit ψ' le morphisme d'anneau de Z/2^rZ dans Z/4Z, sa restriction ψ au groupe des unités est le morphisme recherché.

Le groupe des unités est isomorphe au produit direct du noyau de ψ et du groupe {-1, 1}.

L'application ψ a pour ensemble de départ un groupe d'ordre 2^r-1 et un ensemble d'arrivé un groupe d'ordre 2 car φ(2^r) = 2^r-1 si φ désigne l'indicatrice d'Euler. Ceci démontre que l'ordre du noyau de ψ est égal à 2^r-2. Ce noyau contient 5, en effet ψ(5) = 5ψ(1) = 1 dans (Z/4Z)^*. Toutes les puissances de 5 sont dans le noyaux de ψ car 5 l'est, or la première égalité démontrée dans cette preuve affirme que 5 est d'ordre 2^r-2 car λ est impair. Donc le noyau de ψ est un groupe cyclique d'ordre 2^r-2.

L'élément -1 possède comme image 3 par ψ, il n'est donc pas dans le noyau, le groupe {-1, 1} est d'intersection réduite à l'unité avec le noyau, ils sont donc en somme directe (cf produit direct). le produit des ordre du noyau et de celui du groupe {-1, 1} est égal à l'ordre du groupe des unités, la somme directe est donc égale au groupe des unités, ce qui termine la démonstration.

• Si p est différent de deux, alors le groupe des unités est cyclique.

La démonstration est analogue à la précédente. Pour démontrer cette proposition vérifions d'abord l'égalité suivante par récurrence sur k :

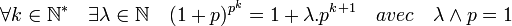
La formule du binôme de Newton montre que, si k est égal à 1, il existe un entier m tel que :

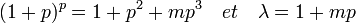
Supposons la propriété vraie à l'ordre k et montrons là à l'ordre k + 1.

Le groupe multiplicatif contient un élément d'ordre p - 1 et un élément d'ordre p^r-1.

L'égalité précédente montre que p + 1 est d'ordre un diviseur de p^r-1 et comme λ est premier avec p son ordre n'est pas un diviseur de p^r-2 son ordre est donc bien p^r-1.

Considérons alors ψ le morphisme surjectif du groupe des unités dans le groupe Z/pZ^*. Son existence est démontrée par un raisonnement analogue au précédent. Le groupe d'arrivée est un groupe cyclique d'ordre p - 1 car p est premier (cf le cas où n est premier). Soit a un antécédent d'un élément générateur du groupe d'arrivée. Il génère un groupe cyclique d'ordre un multiple de p - 1. Ce groupe cyclique donc contient au moins un élément b d'ordre p - 1 et b engendre un groupe cyclique d'ordre p - 1.

Le groupe des unités est cyclique

Considérons un élément de l'intersection des groupes engendrés par b et p + 1. Son ordre est un diviseur de p^r-1 et de p - 1, d'après le théorème de Lagrange. Comme p est premier son ordre est égal à 1, l'intersection est donc réduite à l'unité. Le raisonnement précédent montre que le groupe des unités est le produit direct d'un groupe cyclique d'ordre p - 1 et d'un autre d'ordre p^r-1 car φ(p^r) = (p - 1)p^r-1. De plus les deux groupes cycliques ont deux ordres premiers entre eux, le théorème chinois permet de conclure que le groupe est cyclique, ce qui termine la démonstration.