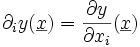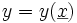Propagation des incertitudes - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Approche mathématique
Notations
- x une variable aléatoire,
- E(x) ou <x> l'espérance mathématique de x,
- V(x) la variance de x.
-
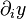
par exemple, si x est un vecteur (x1, x2,…, xn), alors
Formules
Une fonction de variables aléatoires
est elle-même une variable aléatoire. Si les incertitudes sont petites, la variance du développement limité de y au premier ordre autour des valeurs moyennes μ des x est une bonne estimation de la variance de y :
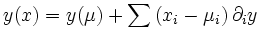
On néglige les termes d'ordre supérieur dans l'expansion, il vient :
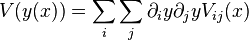
Si les x sont indépendantes
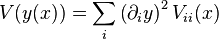
Références externes et notes annexes
- document « Évaluation des données de mesure — Guide pour l’expression de l’incertitude de mesure », JCGM/BIPM, édition 2008, accessible via sa référence "JCGM 100:2008(F) ; ce document et ses recommendations constituent la norme internationale en matière d'incertitudes de mesures ; le document préparatoire ISBN 92-67-10188-9 "ISO Guide to the Expression of Uncertainty in Measurement" fut largement diffusé, et est ainsi souvent référencé sous l'acronyme de GUM. L'annexe B, "Termes métrologiques généraux" définit précisément les termes d'erreur et d'incertitude.
- ce terme de "demie-incertitude" est totalement impropre à l'usage, et n'a ici qu'une valeur de clarification ou d'image pédagogique