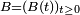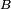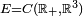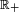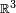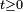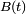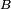Variable aléatoire - Définition

Introduction

Une variable aléatoire est une fonction définie sur l'ensemble des éventualités, c'est-à-dire l'ensemble des résultats possibles d'une expérience aléatoire.

Une variable aléatoire est souvent à valeurs réelles (gain d'un joueur dans un jeu de hasard, durée de vie) et on parle alors de variable aléatoire réelle : . La variable aléatoire peut aussi associer à chaque éventualité un vecteur de ou , et on parle alors de vecteur aléatoire : ou . La variable aléatoire peut encore associer à chaque éventualité une valeur qualitative (couleurs, Pile ou Face), ou même une fonction (p.e. une fonction de ), et on parlera alors de processus stochastique.

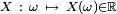
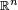
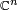
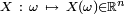
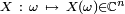
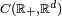
Ce furent les jeux de hasard qui amenèrent à concevoir les variables aléatoires, en associant à une éventualité (résultat du lancer d'un dé, d'un tirage à pile ou face, d'une roulette, ...) un gain. Cette association éventualité-gain amena à concevoir une fonction de manière plus générale à partir d'une éventualité. Le développement des variables aléatoires est associé à la théorie de la mesure .

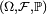
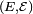
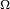
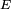
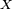
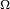
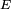
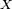
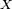
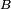
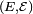
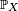
Cette condition de mesurabilité de assure que l'image réciproque par de tout élément de la tribu possède une probabilité et permet ainsi de définir, sur , une mesure de probabilité, notée , par

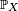
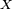
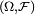
La mesure est l'image, par l'application , de la probabilité définie sur .

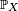
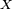
Exemples

Dans la suite, désigne la tribu borélienne de l'espace topologique .

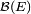
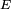
• Lorsque , on dit que est une variable aléatoire réelle.
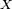
• Lorsque, pour un entier , , on dit que est un vecteur aléatoire.
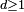
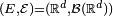
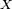
• Lorsqu'il existe un ensemble fini ou dénombrable tel que , on dit que est une variable discrète. Par exemple, le choix permet de voir les variables aléatoires suivant la loi de Poisson ou la loi binomiale comme des variables aléatoires réelles.
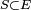
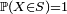
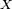
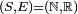
• Le mouvement brownien , qui modélise la trajectoire de certaines particules dans l'espace, peut être vu comme une variable aléatoire à valeurs dans l'espace des fonctions continues de dans muni de la topologie de la convergence uniforme sur tout compact, et de la tribu borélienne correspondante. Pour chaque , , qui représente la position de la particule à l'instant , est une variable aléatoire réelle dont la loi est gaussienne. Ainsi peut aussi être vu comme une famille de variables aléatoires réelles.