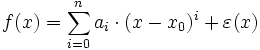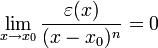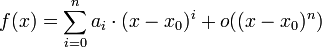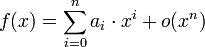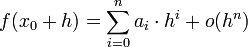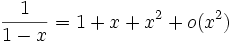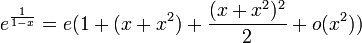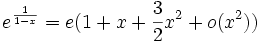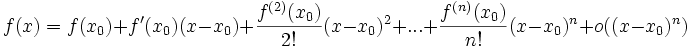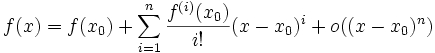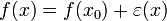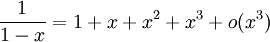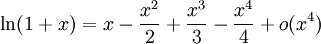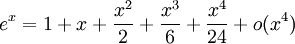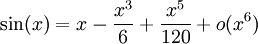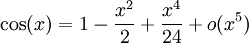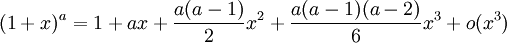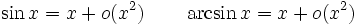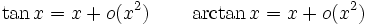Développement limité - Définition
En physique et en mathématiques, un développement limité d'une fonction f au voisinage de x0, est l'écriture d'une fonction sous la forme d'une fonction polynôme et d'un reste
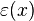
Il se révèle très utile quand on recherche l'approximation d'une fonction au voisinage d'un point ou un équivalent de celle-ci.
En physique, il est fréquent de confondre la fonction avec son développement limité à condition que l'erreur ainsi faite soit inférieure à l'erreur autorisée. Si l'on se contente d'un développement d'ordre 1, on parle d'approximation linéaire.
En mathématiques, les développements limités permettent de trouver plus simplement des limites de fonctions, de calculer des dérivées ou d'étudier des positions de courbes par rapport à des tangentes.
L'étude des développement limités se prolonge par l'étude des développements en séries entières.
Définitions
On dit que la fonction f possède un développement limité d'ordre n (abrégé par la suite en D.L.n) au voisinage I de x0 s'il existe n + 1 réels a0, …, an et une fonction ε(x), tels que, pour tout x de I :
la fonction ε(x) tendant vers 0 lorsque x tend vers un point x0, et ce " plus rapidement " que le dernier terme de la série, c'est-à-dire que :
Les fonctions vérifiant ceci sont notées o((x – x0)n), on écrit donc :
Le nombre n est appelé ordre de développement.
Il est fréquent de chercher plutôt un développement limité au voisinage de 0 dont l'expression se trouve être plus simple :
il est facile d'y parvenir en posant le changement de variable x = x0 + h
On prouve que si une fonction admet un D.L.n au voisinage de x0, ce développement est unique. On prouve aussi que a0 = f(x0).
Note : la fonction f peut être à valeurs vectorielles.
Opérations sur les développements limités
- Somme
- Si ƒ et g possèdent deux D.L.n, alors ƒ + g possède un D.L.n qui s'obtient en effectuant la somme des deux polynômes.
- Multiplication par λ
- si ƒ possède un D.L.n alors λ·ƒ aussi, obtenu en multipliant le D.L.n de ƒ par λ.
- Produit
- Si ƒ et g possèdent des D.L.n, alors ƒ·g possède un D.L.n. Si ak, bk et ck sont les coefficients de xk dans les développements respectifs de ƒ, g et ƒ·g, le coefficient ck est obtenu par la formule suivante :
-
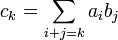
- Inverse
- Si u(x0) = 0 et si u possède un D.L.n au voisinage de x0, alors
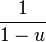
-
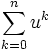
- Composition
- si u possède un D.L.n au voisinage de x0 et si v possède un D.L.n au voisinage de u(x0), alors v o u possède un D.L.n qui s'obtient en cherchant un D.L.n de Qn o Pn où Pn et Qn sont les D.L.n de u et v
- ex : développement limité d'ordre 2 au voisinage de 0 de
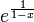
- D.L.2au voisinage de 1 de ex :
-
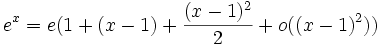
- rem: le D.L. au voisinage de 1 de ex se trouve en remarquant que ex = e.ex − 1 et en utilisant le D.L. de eh au voisinage de 0
-
- D.L.2 au voisinage de 0 de
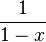
-
- D.L.2 au voisinage de 0 de
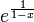
-
- Intégration
- Si ƒ est continue sur un intervalle I autour x0 et possède un D.L.n au voisinage de x0, alors toute primitive F de ƒ possède un D.L.n+1 au voisinage de x0 qui est
-
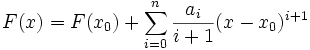
- Dérivation
- il n'existe pas de théorème général sur l'existence d'un D.L.n - 1 pour la dérivée d'une fonction admettant un D.L.n au voisinage de x0.
- par exemple la fonction définie par
-
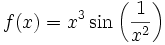
-
- possède un développement limité d'ordre 2 au voisinage de 0 mais sa dérivée, non continue, ne possède pas de D.L.1 .
- Par contre si f' admet un D.L d'ordre n-1 en xo alors la partie régulière du D.L de f' est la dérivée de la partie régulière du D.L d'ordre n de f en xo .
D.L.n et fonctions dérivables
Article principal: Théorème de Taylor
Le mathématicien Taylor a démontré qu'une fonction f, dérivable n fois sur un intervalle I contenant x0, possédait un D.L.n au voisinage de x0 :
soit en écriture abrégée
En revanche, le fait qu'une fonction possède un D.L.n au voisinage de x0 n'assure pas que la fonction soit n fois dérivable en x0. On peut juste déduire, de l'existence d'un D.L.0 au voisinage de x0, la continuité en x0, et, de l'existence d'un D.L.1 au voisinage de x0, la dérivabilité en x0. Par contre si f' admet un D.L d'ordre n-1 en xo alors la partie régulière du D.L de f' est la dérivée de la partie régulière du D.L d'ordre n de f en xo .
Quelques utilisations
Le développement d'ordre 0 consiste à considérer que ƒ est continue en x0 :
Le développement limité d'ordre 1 consiste à approcher une courbe par sa tangente ; on parle aussi d'approximation linéaire :
-
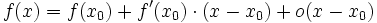
Son existence équivaut à la dérivabilité de la fonction en x0.
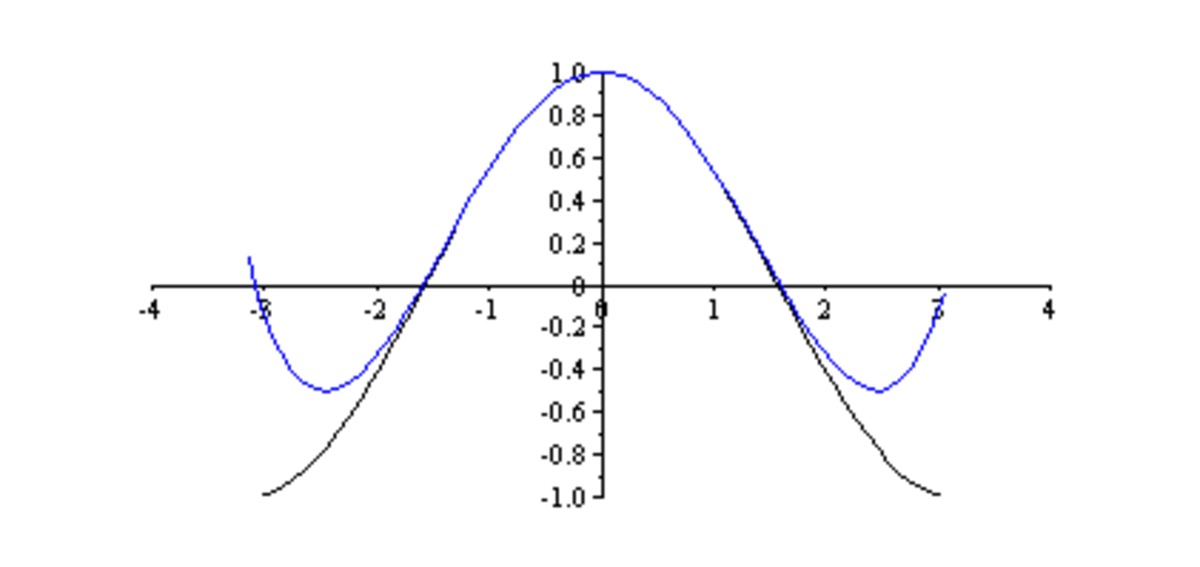
Le développement limité d'ordre 2 consiste à approcher une courbe par une parabole, ou loi quadratique. Il permet aussi de préciser la position de la courbe par rapport à sa tangente, au voisinage du point de contact (pourvu que le coefficient du terme de degré 2 soit non nul).
Le changement de variable
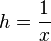
Quelques exemples
Les fonctions suivantes possèdent des D.L.n au voisinage de 0 pour tout entier n et sont développables en séries entières.
-
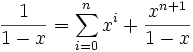
- par intégration de la formule précédente et changement de x en -x
-
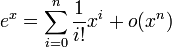
-
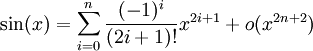
-
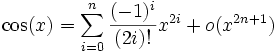
-
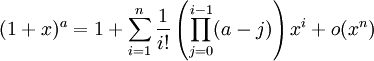
Voir l'article série entière.
Applications
Pour ces mêmes fonctions, voici quelques applications des formules précédentes à des ordres couraments utilisés :
Approximations linéaires : développements limités d'ordre 1 en physique
En physique, on utilise fréquemment des développements limités d'ordre 1 :
- en 0 :
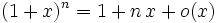
-
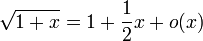
-
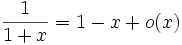
-
- toute forme de type (a + x),
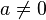
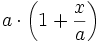
- en 0 : fonctions trigonométriques
-