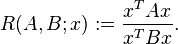Quotient de Rayleigh - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Généralisation
On peut étendre la notion de quotient de Rayleigh à deux matrices symétriques définies positives réelles (A,B), et à un vecteur non-nul x, selon :
Ce « quotient de Rayleigh généralisé » se réduit au quotient de Rayleigh R(D,Cx) par la transformation D = C − TAC − 1 où C est la factorisation de Cholesky de la matrice B.