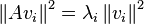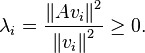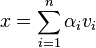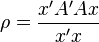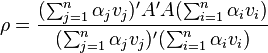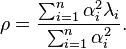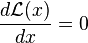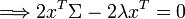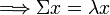Quotient de Rayleigh - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le quotient de Rayleigh est un nombre réel caractérisant l'effet d'une matrice symétrique (respectivement hermitienne) sur un vecteur, et offrant les deux propriétés fondamentales suivantes :
- le quotient de Rayleigh atteint un extremum relatif pour les vecteurs propres de la matrice
- l’application du quotient de Rayleigh à un vecteur propre donne la valeur propre correspondante.
Ces deux propriétés peuvent servir à déterminer numériquement les Valeur propre, vecteur propre et espace propre d'un opérateur hermitien ou symétrique.
Le quotient de Rayleigh, dont la propriété d'extremum peut être reliée au principe du minimum de l'énergie potentielle en mécanique, a été étudié pour la première fois par Rayleigh (1877). Walter Ritz reprit l'idée en 1909 pour en faire la base d’une méthode d’approximation variationnelle.
Définitions et propriétés caractéristiques
En mathématiques, pour une matrice hermitienne A à coefficients complexes et un vecteur x non nul, on appelle quotient de Rayleigh R(A,x) le scalaire :
où x * désigne le vecteur adjoint de x, c'est-à-dire le conjugué du vecteur transposé.
Pour des matrices et des vecteurs à coefficients réels, le caractère hermitien se traduit par la caractère symétrique, et il faut substituer à la matrice adjointe x * la transposée familière x'. Notez que
- pour tout nombre réel c, R(A,cx) = R(A,x).
Rappelons également que les valeurs propres d'une matrice symétrique (respectivement hermitienne) sont toutes réelles. On peut montrer que, sous ces conditions,
- le quotient de Rayleigh atteint un minimum
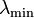
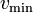
- En outre,
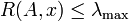
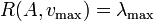
Méthode de Rayleigh-Ritz
La Théorie de Sturm-Liouville a trait à l’action de l’application linéaire
sur l’espace préhilbertien des fonctions y(x) vérifiant des conditions aux limites particulières en x=a et b, muni du produit scalaire :
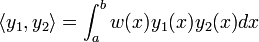
Dans ce cas, le quotient de Rayleigh est
On le présente parfois sous une forme équivalente, obtenue en découpant l'intégrale du numérateur et en intégrant par parties :
Pour déterminer une solution approchée
vérifiant les conditions aux limites, on choisit un certain nombre de fonctions u1,u2,...,up vérifiant elles-mêmes les conditions aux limites, et on cherche la solution approchée comme une combinaison linéaire des p modes retenus :
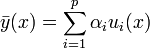
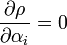
Cas particulier des matrices de covariance
On peut factoriser une matrice de covariance Σ sous la forme A'A. Les valeurs propres d'une telle matrice sont positives, car :
- Σvi = λivi
- A'Avi = λivi
- vi'A'Avi = vi'λivi
Les vecteurs propres sont deux à deux orthogonaux :
- Σvi = λivi
- vj'Σvi = λivj'vi
- (Σvj)'vi = λivj'vi
- λjvj'vi = λivj'vi
- (λj − λi)vj'vi = 0
- vj'vi = 0 (pour des valeurs propres différentes ; en cas de multiplicité, la base de Im(Σ) peut être orthogonalisée).
Disposant donc d'une base, on peut exprimer le quotient de Rayleigh en fonction des valeurs propres en décomposant un vecteur quelconque x sur cette base des vecteurs propres :
relation qui, de par l’orthogonalité des vecteurs propres, devient :
Si un vecteur x rend maximal le scalaire ρ, alors tout vecteur k.x (car
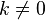
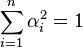
Par la relation ci-dessus, il apparaît que la recherche d'un vecteur propre se ramène à la recherche d'un extremum de Lagrange, à savoir
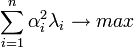
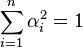
Puisque toutes les valeurs propres sont positives, le problème est convexe et le maximum est atteint à la frontière du domaine, à savoir quand α1 = 1 et  (en supposant que les valeurs propres soit numérotées par ordre de valeur décroissante).
(en supposant que les valeurs propres soit numérotées par ordre de valeur décroissante).
On aboutit au même résultat par la méthode des multiplicateur de Lagrange. Le problème consiste alors à déterminer les points critiques de la fonction
- ρ(x) = xTΣx, sous la contrainte
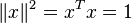
c’est-à-dire trouver les points critiques de
-
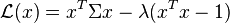
où λ est un multiplicateur de Lagrange. Les points stationnaires de
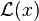
et
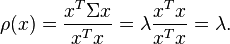
Par conséquent, les vecteurs propres
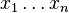
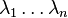
Cette propriété remarquable est à la base de l’analyse en composantes principales et des corrélations canoniques.
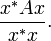
![L(y) = \frac{1}{w(x)}\left(-\frac{d}{dx}\left[p(x)\frac{dy}{dx}\right] + q(x)y\right)](https://static.techno-science.net/illustration/Definitions/autres/f/f7a279e06daa340e9ecd72639b512b93_9e6e8fe335aeef04ee9a6eb1fd08a44e.png)
![\rho(x) =\frac{\langle{y,Ly}\rangle}{\langle{y,y}\rangle} = \frac{\int_a^b{y(x)\left(-\frac{d}{dx}\left[p(x)\frac{dy}{dx}\right] + q(x)y(x)\right)}dx}{\int_a^b{w(x)y(x)^2}dx}.](https://static.techno-science.net/illustration/Definitions/autres/f/ff2dddef1b00e4311d5c13d116ea4834_761b21b69158622ebb85040318000c65.png)
![\rho(x) =\frac{\langle{y,Ly}\rangle}{\langle{y,y}\rangle} = \frac{\int_a^b{y(x)\left(-\frac{d}{dx}\left[p(x)y'(x)\right]\right)}dx + \int_a^b{q(x)y(x)^2}dx}{\int_a^b{w(x)y(x)^2}dx}](https://static.techno-science.net/illustration/Definitions/autres/9/92381da7a988416645f744e5c8b67b9d_6598105a5e135e640f79da9f81b4a392.png)
![= \frac{-y(x)\left[p(x)y'(x)\right]|_a^b + \int_a^b{y'(x)\left[p(x)y'(x)\right]}dx + \int_a^b{q(x)y(x)^2}dx}{\int_a^b{w(x)y(x)^2}dx}](https://static.techno-science.net/illustration/Definitions/autres/1/128eb1b1ef232187728a6dbc8924e085_39a42b5d8c8706c86376ba40c3caba00.png)
![= \frac{-p(x)y(x)y'(x)|_a^b + \int_a^b\left[p(x)y'(x)^2 + q(x)y(x)^2\right]dx}{\int_a^b{w(x)y(x)^2}dx}.](https://static.techno-science.net/illustration/Definitions/autres/8/88c7efb4d53dffa54ce9f9b915b91499_a92d002935009d6e48a1be3c77bd5cd6.png)
![-\frac{d}{dx}\left[p(x)\frac{dy}{dx}\right] + q(x)y = 0](https://static.techno-science.net/illustration/Definitions/autres/6/65804be6903371f448f2719062c47572_912e25cb8df729b668cf14ec52dd74b1.png)