Représentation de groupe - Définition

Introduction

L'idée générale de la théorie des représentations est d'essayer d'étudier un groupe G en le faisant agir sur un espace vectoriel V de manière linéaire : on essaie ainsi de voir G comme un groupe de matrices (d'où le terme représentation). On peut ainsi, à partir des propriétés relativement bien connues du groupe des automorphismes de V, arriver à déduire quelques propriétés de G.

Quelques définitions

Définition la plus élémentaire

Cas général

Soit G un groupe, K un corps et V un espace vectoriel sur K. On appelle représentation de G un morphisme de groupe de G dans GL(V), autrement dit, une application telle que ρ(g₁)ρ(g₂) = ρ(g₁g₂), c'est-à-dire que l'application préserve la loi du groupe.

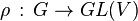
Pour écrire l'action d'un élément g du groupe sur un élément v de l'espace vectoriel à travers la représentation ρ, on notera parfois ρ(g)(v), ρ(g).v ou même g.v s'il n'y a aucune ambiguïté. On note parfois une représentation (V,ρ). On dit parfois également (et abusivement) que V est une représentation de G.

On dit que la représentation est fidèle si le morphisme ρ est injectif. Si par ailleurs V est de dimension finie (cas le plus fréquent), cette représentation permet alors de voir G comme un groupe de matrices. La dimension de V est alors appelée degré de la représentation. Si V est de dimension infinie, alors les ρ(g) sont des opérateurs linéaires.

Exemples :

• Soit G le groupe constitué des éléments {1,-1} et V un espace vectoriel quelconque. On peut construire une représentation de G en prenant ρ(1) = Id_V et ρ( − 1)(x) = − x pour .
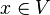
• Soit G le groupe des rotations de . Puisque G est déjà inclus dans GL(3), l'identité sur G définit une représentation triviale de G sur . Une autre représentation peut être trouvée dans le cas où V est un espace de fonctions définies sur , en notant , avec . L'image d'une fonction f par est en effet la fonction , et l'application ρ définit un morphisme de groupes.

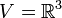
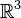
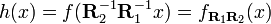
Cas des groupes topologiques : représentation continue

Si G est un groupe topologique et V a une topologie, la représentation ρ est une représentation continue si l'application Φ de dans V définie par est continue. En particulier (et c'est très utile dans le cas des groupes compacts), pour tout l'application est continue.

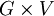
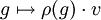
Action de groupe fortement continue et points réguliers

Si est une action d'un groupe topologique G sur un espace topologique X, on dit que celle-ci est fortement continue si quel que soit , l'application est continue pour les deux topologies considérées. Une telle action induit une action sur l'espace des fonctions continues sur X : il suffit de poser .

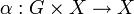
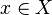
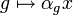
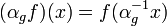
Le sous-espace des points réguliers pour l'action α est le sous-espace de X des points x tels que est régulière, c'est-à-dire continue avec toutes ses dérivées continues.

Définition plus savante

K-algèbre d'un groupe

Notons K[G] le K-espace vectoriel engendré par les éléments de G (c’est-à-dire l'ensemble des combinaisons linéaires formelles finies à coefficients dans K des éléments de G). Un élément générique de K[G] s'écrit

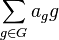
où les a_g sont des éléments de K tous nuls sauf un nombre fini d'entre eux (la somme est donc finie) et où les lettres g sont à considérer comme des symboles formels.

On peut donner à K[G] une structure d'anneau (et donc de K-algèbre) en le munissant de la loi de multiplication (naturelle) suivante :

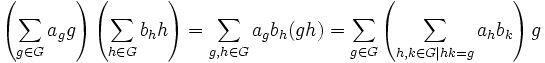
où toutes les sommes sont en fait finies.

K[G] s'appelle la K-algèbre du groupe G.

Lien avec les représentations

On peut alors étendre, et ce de façon unique, la représentation ρ à un morphisme de K-algèbres de K[G] vers End(V), en posant . Ceci fait de V un K[G]-module. On dit également que V est un G-module.

Réciproquement, la donnée d'un K[G]-module V fournit une représentation de G.

Morphismes

Un morphisme entre deux représentations (V,ρ) et (W,σ) est simplement une application K-linéaire de V dans W telle que pour tout g appartenant à G on ait

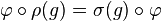
On dit alors aussi que est un morphisme G-équivariant.

Deux représentations sont dites semblables, ou isomorphes lorsqu'il existe un isomorphisme G-équivariant entre les espaces correspondants. Il est alors possible de les identifier.