Espace topologique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La topologie générale est une branche des mathématiques qui fournit un vocabulaire et un contexte général pour traiter des notions de limite, de continuité, dans le cadre d'un continuum ou d'un espace discret, voire fini. Dans ce contexte, les espaces topologiques forment le socle conceptuel dans lequel ces notions sont définies. Le cadre est suffisamment général pour s'appliquer à un grand nombre de situations différentes : ensembles finis, discrets, espaces de la géométrie euclidienne, espaces numériques à n dimensions, espaces fonctionnels les plus complexes et géométrie algébrique. Ces concepts apparaissent dans presque toutes les branches des mathématiques ; ils sont donc centraux dans la vision moderne des mathématiques. La branche des mathématiques qui étudie ces espaces s'appelle la topologie.
La topologie générale ne tente pas d'élucider la question très complexe de la « composition du continu » : elle part d'une approche axiomatique, en utilisant le vocabulaire de la théorie des ensembles ; autrement dit, elle suit une approche fondée sur une notion de structure (en l'occurrence, ici, une structure topologique), en faisant usage d'une axiomatique ensembliste. Les axiomes sont minimaux, et en ce sens c'est la structure la plus générale pour étudier les concepts cités. Ils ont été formalisés par Kolmogorov au début du XXe siècle.
La topologie générale, en elle même, s'attache à définir le vocabulaire. Elle possède deux branches importantes : la topologie différentielle et la topologie algébrique, où la notion générale de « forme » est étudiée avec un degré de complexité et d'approfondissement extrêmes.
Cet article est technique, une vision générale et historique est donnée dans Topologie.
Concepts
Définitions
Un espace topologique est un couple (E,Τ), où E est un ensemble et Τ un ensemble de parties de E que l'on définit comme les ouverts de (E,Τ), vérifiant les propriétés suivantes :
-
- L'ensemble vide et

- Toute réunion d'ouverts est un ouvert, c'est-à-dire si
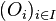
-
-
-
-
-
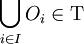
-
-
-
-
-
- Toute intersection finie d'ouverts est un ouvert, c'est-à-dire si
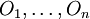
-
-
-
-
-
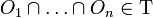
-
-
-
-
-
- L'ensemble vide et
L'ensemble Τ, qui est un ensemble de parties de E, est alors appelé une topologie sur E.
Un fermé d'une topologie est défini comme le complémentaire d'un ouvert. Par conséquent, la famille des fermés contient E et l'ensemble vide. Il résulte de la théorie élémentaire des ensembles que toute intersection de fermés est un fermé et que toute réunion finie de fermés est un fermé.
Il est d'usage de rappeler la présence de la partie vide à la propriété 1 ; c'est toutefois en toute rigueur superflu, puisqu'on peut l'obtenir en appliquant la propriété 2 à la réunion indexée par l'ensemble vide.
Un des premiers rôles de la topologie est de décrire les voisinages des points. C'est une notion-clé pour comprendre la topologie. Elle sert par exemple à la définition de continuité ou de limite en un point. Cette notion est formalisée dans l'article voisinage. Rappelons ici simplement qu'une partie de E est un voisinage d'un point si elle contient un ouvert contenant ce point.
Exemples
- Un exemple simple est
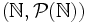
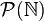
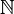

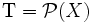
- La topologie grossière sur


- Un exemple sur les entiers est
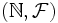
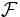
- L'article sur les voisinages démontre qu'il existe une topologie associée à tout espace métrique. Un ouvert
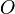

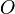

- L'ensemble des nombres réels est donc muni naturellement d'une topologie issue de sa distance. Un ouvert est alors une union d'intervalles ouverts.
- La topologie produit est une topologie définie sur un produit cartésien d'espaces topologiques. Un exemple simple est donnée par les espaces vectoriels de dimension finie réels ou complexes. La topologie produit s'applique aussi aux espaces vectoriels de dimension infinie, on obtient alors la topologie de la convergence simple.
- La topologie induite d'un sous-ensemble
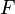


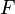


- Tout ensemble ordonné peut être muni de topologies liées à l'ordre. La topologie la plus commune s'appelle topologie de l'ordre.
- D'autres exemples de topologies plus sophistiquées sont donnés dans l'article voisinage.
- Le cube de Hilbert
![[0,1]^\N](https://static.techno-science.net/illustration/Definitions/autres/8/87018ac4548501371d4f40dc5e7d0c8f_15f275f7db35fb316a0d384444b8ad0b.png)
- L'ensemble de Cantor est source de nombreux exemples et contre-exemples.
Topologie engendrée par une famille de fonctions
- Soient X un ensemble quelconque, Y un espace topologique et f une fonction de X dans Y. On peut alors définir sur X une topologie particulière liée à ce système. C'est la plus petite topologie (ou la plus grossière) sur X rendant f continue.
- De même, si f était de Y dans X, on définirait sur X la topologie la plus grande (ou la plus fine) telle que f soit continue.
On peut généraliser ces deux définitions en remplaçant l'espace Y par une famille d'espaces (Yi)i∈I, et l'application f par une famille d'applications (fi)i∈I.

















































