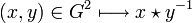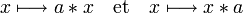Groupe topologique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, un groupe topologique est un groupe muni d'une topologie compatible avec la structure de groupe, c'est-à-dire lorsque la loi de composition interne du groupe et le passage à l'inverse sont deux applications continues.
L'étude des groupes topologiques mêle donc des raisonnements d'algèbre et de topologie. La structure de groupe topologique est une notion essentielle en topologie algébrique.
Définition et propriété caractéristique
Définition — Un groupe
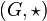
-
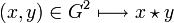
- et
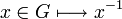
sont continues.
Les deux axiomes de la définition peuvent être remplacés par un seul :
Exemples de base
Théorème : Le groupe additif


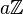
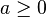
Démonstration :
Soit
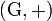
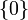
![G^{+} = G \cap ]0;+\infty[](https://static.techno-science.net/illustration/Definitions/autres/d/dff5899acd028a671fb42fd57349a000_206ef85b86b2cbb2b41830c977a033af.png)
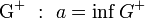
Si
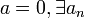
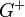
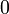
![\varepsilon > 0 , \exists x \in G \cap ]0;\varepsilon[](https://upload.wikimedia.org/math/8/d/c/8dc882e30b4e8d5b8b7de9f926182d12.png) tel que
tel que
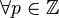
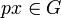

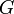
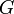
Si
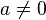
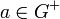
![(\forall \varepsilon > 0)(\exists(x,y) \in G^{+} ) \big((x,y) \in ]a;a+ \varepsilon [^2\ et\ x < y \bigr)](https://upload.wikimedia.org/math/f/e/d/fed7767b12da570216e045adf4ed45f2.png) (car il y a une infinité d’éléments de
(car il y a une infinité d’éléments de
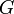
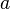
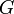
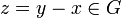
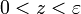
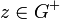
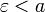
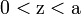
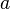
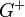
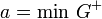
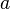
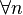
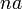
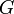
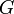
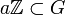
Soit
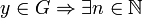
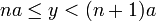

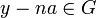
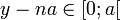
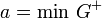
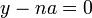
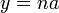
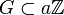
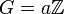
Le cercle
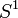
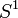
Un exemple plus sophistiqué est
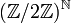
Mesure de Haar
Sur tout groupe topologique localement compact et séparable, il existe une et une seule mesure (à coefficient multiplicateur près) invariante par la translation à gauche
Groupes linéaires
Dorénavant, nous omettrons le signe
Une classe importante de groupes topoloqiques est formée par les sous-groupes du groupe linéaire
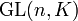
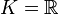

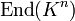
Ces exemples sont des exemples fondamentaux de groupes de Lie réels ou complexes. Ils ont en commun la propriété suivant : il existe un ouvert contenant l'élement neutre et ne contenant aucun sous-groupe non trivial.
Quelques propriétés générales
Dans un groupe topologique, les translations
sont des homéomorphismes.
La topologie est déterminée par la donnée des voisinages de l'élément neutre e.
Un groupe topologique G est séparé ssi le singleton {e} est fermé dans G. Également, G est séparé ssi l'intersection des voisinages de e est réduite à {e}.
- si G est séparé alors c'est a fortiori un espace T1, c'est-à-dire que tous ses singletons sont fermés, en particulier le singleton {e}.
- Réciproquement, si {e} est fermé alors G est séparé puisque la diagonale de GxG est fermée, comme image réciproque de {e} par l'application continue qui à tout (x,y) associe x.y-1.
- Si G est séparé alors c'est un espace T1, c'est-à-dire que l'intersection des voisinages de tout point x est réduite à {x}, en particulier pour x=e.
- Réciproquement, si l'intersection des voisinages de e est réduite à {e} alors {e} est égal à son adhérence donc fermé (donc, d'après ce qui précède, G est séparé). En effet, pour tout x adhérent à {e}, chaque voisinage de x contient e donc (par continuité de la translation) chaque voisinage de e contient x-1, d'où x-1=e, c'est-à-dire x=e.
Si
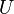
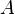
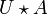
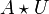
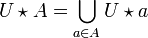
Un groupe topologique est naturellement muni de deux structures uniformes (à droite et à gauche) qui induisent sa topologie, et qui coïncident si le groupe est commutatif. Un groupe topologique séparé est par conséquent complètement régulier. Tout morphisme continu de groupes topologiques est uniformément continu pour les structures uniformes à droite (resp. gauche) associées.