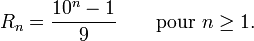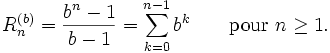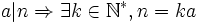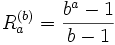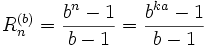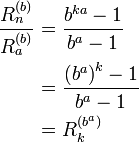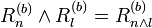Répunit - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Définition - Répunits premiers

Introduction

Dans le domaine des mathématiques récréatives, un répunit est un nombre entier dont l'écriture ne comporte que des chiffres 1. Ce terme est une contraction de l'expression anglaise repeated unit (répétition de l'unité), utilisée pour la première fois en 1966 par Albert H. Beiler.

En français ont été proposés « nombres polymonadiques », ou « multi-as », mais c'est l'anglicisme qui est le plus utilisé.

Définition

Les répunits sont définis en base 10 par :

Plus généralement, en base b, les répunits sont donnés par

Ainsi, le nombre $R_n^{(b)}$ s'écrit comme la juxtaposition de n chiffres 1

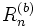
Exemples

Les premiers termes de la suite des répunits sont :

1, 11, 111, 1 111, 11 111, 111 111, 1 111 111 (suite A002275 de l'Encyclopédie électronique des suites entières).

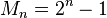
Les répunits en base 2 (répunits binaires) sont les valeurs de la suite $M_n=2^n-1\,$ .

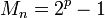
Les nombres de Mersenne ( $M_n=2^p-1\,$ avec $p$ un nombre premier) sont des répunits binaires.

Répunits premiers

Historiquement, c'est dans le cadre des mathématiques récréatives qu'a été entreprise l'étude des répunits, en tentant notamment de les factoriser. Le projet Cunningham se propose de répertorier les factorisations des répunits en base 2, 3, 5, 6, 7, 10, 11, et 12.

On montre aisément que si n est divisible par a, alors R_n est divisible par R_a.

Soient trois entiers b, a et n tels que 0 < a < n et b > 1.
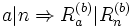
Montrons $a|n \Rightarrow R_a^{(b)}|R_n^{(b)}$ :

Calculons le rapport entre ces deux répunits :

\begin{align}\frac{R_n^{(b)}}{R_a^{(b)}}&= \frac{b^{ka}-1}{b^a-1} \\ \ & = \frac{{(b^a)}^k-1}{b^a-1} \\ \ & = R_k^{(b^a)} \end{align}

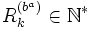
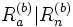
Or $R_k^{(b^a)}\in\mathbb{N}^*$ , et donc $R_a^{(b)}|R_n^{(b)}$ CQFD

Pour s'imaginer la chose, on peut se représenter qu'une répétition de $n = k a$ unités est aussi une juxtaposition de $k$ paquets de $a$ unités.

Par exemple, 9 est divisible par 3, et R₉ est bien divisible par R₃ :

111 111 111 = 111 · 1 001 001.

Plus généralement :

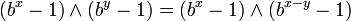
$(b^x-1) \wedge (b^y-1) = (b^x-1)\wedge(b^{x-y}-1)$

Ainsi, R_n n'est premier que si n est premier. Mais ce n'est pas une condition suffisante, comme l'illustre ce contre-exemple :

3 est premier mais R₃ = 111 = 3 · 37 est composé

Les répunits premiers sont assez rares (la probabilité qu'un nombre soit premier est a priori égale à son logarithme). On conjecture cependant qu'il en existe une infinité.

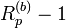
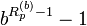
Ce qu'il faut noter, par rapport au petit théorème de Fermat, lorsque p est premier : p divise $R_p^{(b)}-1$ donc $b^{R_p^{(b)}-1}-1$ est divisible par $R_{p}^{(b)}$

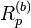
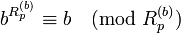
$b^{R_p^{(b)}} \equiv b \pmod{R_p^{(b)}}$ lorsque p est premier

En base 10, R_n est premier pour n = 2, 19, 23, 317, 1031,... (suite A004023 de l'Encyclopédie électronique des suites entières). R₄₉₀₈₁, R₈₆₄₅₃, R₁₀₉₂₉₇ et R₂₇₀₃₄₃ sont des nombres premiers probables.

Les répunits premiers constituent un sous-ensemble des nombres premiers permutables, c'est-à-dire des nombres premiers qui demeurent premiers après toute permutation de leurs chiffres.

Étant donné un entier n que ne divisent ni 2 ni p, il existe un répunit de base 2p multiple de n.

- Introduction - Définition - Répunits premiers