Tas de Fibonacci - Définition

Analyse du pire cas

Bien que le temps d'exécution total d'une séquence d'opérations en partant d'une structure vide soit borné par les valeurs données plus haut, quelques opérations dans la séquence (très peu) peuvent prendre un temps très long (en particulier diminuer clé, supprimer et supprimer minimum ont des temps d'exécution linéaires dans le pire cas). Pour cette raison, les tas de Fibonacci, ainsi que d'autres structures optimisées au niveau de leur coût amorti mais pas de leur pire cas, peuvent être mal appropriés à certaines applications temps réel.

Implémentation des opérations

Pour permettre la suppression rapide et la concaténation, les racines de tous les arbres sont liées par une liste doublement chaînée circulaire. Les fils de chaque nœud sont aussi liés par une liste du même type. Pour chaque nœud, on conserve des informations sur son nombre de fils et sur son marquage éventuel. De plus, on garde un pointeur sur la racine contenant la clé minimale.

L'opération trouver le minimum est maintenant triviale, puisqu'on garde un pointeur sur son nœud. Cette opération ne change pas le potentiel du tas, et donc le coût réel et le cout amorti sont constants. Comme mentionné plus haut, l'union est implémentée simplement en concaténant les listes des racines des arbres des deux tas. Cette opération peut être effectuée en temps constant et le potentiel ne change pas, et donc le temps amorti est encore constant. L'opération insertion crée un nouveau tas avec le seul élément à insérer, et effectue l'union avec le tas de départ. Ceci prend un temps constant, mais ici le potentiel augmente d'une unité, car le nombre d'arbres augmente. Le coût amorti est donc toujours constant.

Le tas de Fibonacci de la figure 1 après la première phase de l'extraction du minimum. Le nœud avec la clé 1 (le minimum) a été supprimé et ses fils ont été ajoutés comme arbres séparés.

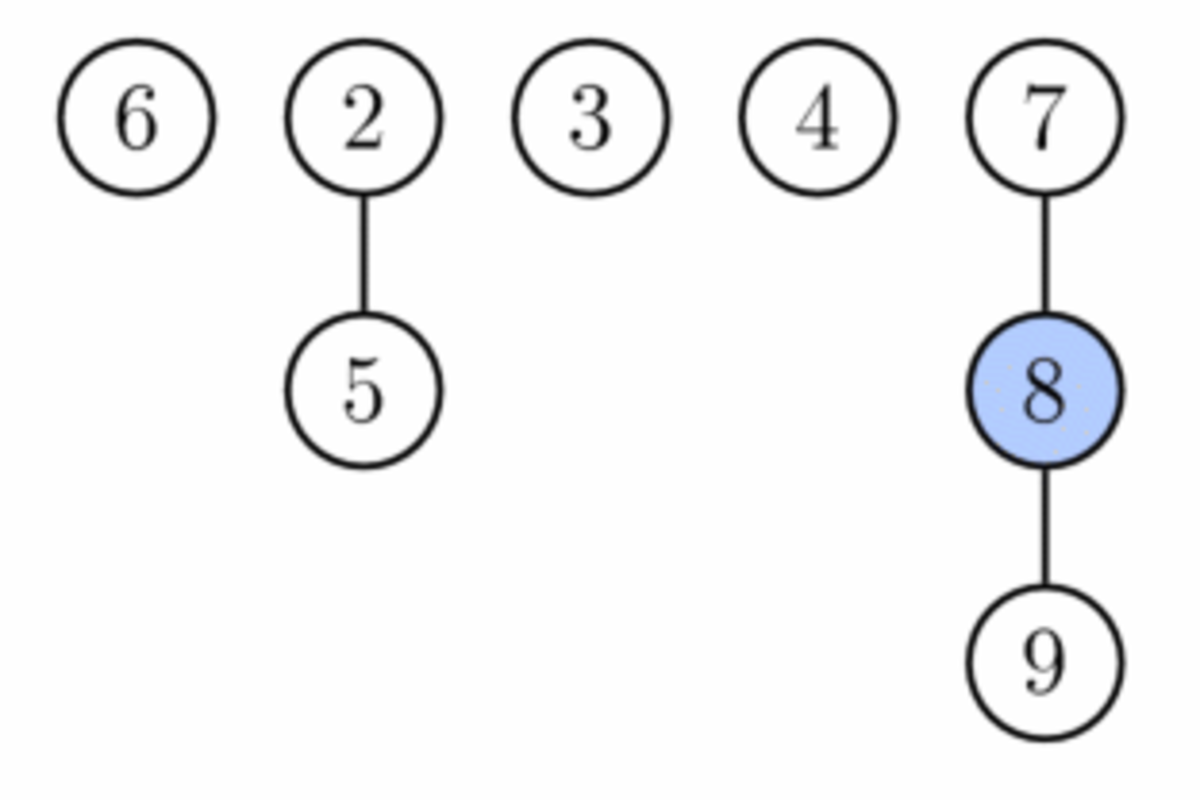
L'opération extraire le minimum (de même que supprimer le minimum) opère en trois phases. D'abord, on prend la racine contenant l'élément minimum et on la supprime. Ses fils vont devenir les racines de nouveaux arbres. Si le nombre de fils était d, il faut un temps O(d) pour traiter toutes les nouvelles racines et la fonction de potentiel augmente de d-1. Donc le coût amorti de cette phase est O(d) = O(log n).

Le tas de Fibonacci de la figure 1 après la fin de l'opération extraire minimum. D'abord les nœuds 3 et 6 sont connectés, puis le résultat est connecté avec l'arbre de racine 2. Enfin, le nouveau minimum est trouvé.

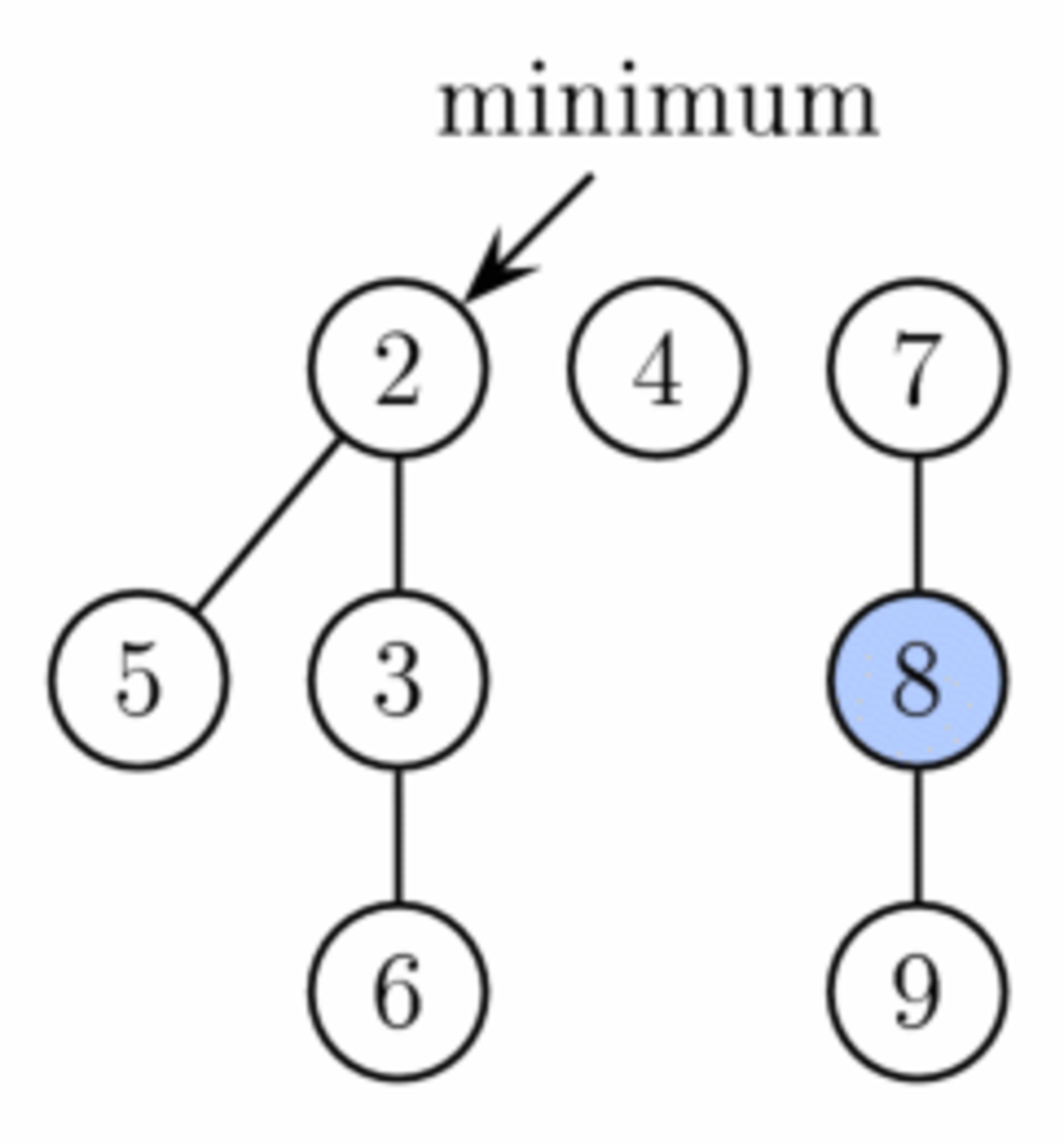
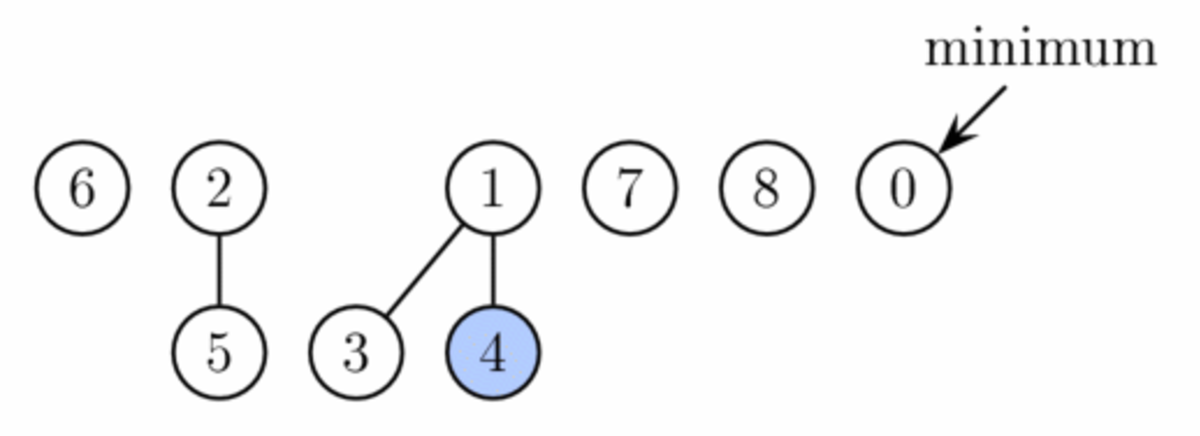
Cependant, pour finir l'opération d'extraction du minimum, on doit mettre à jour le pointeur sur la racine de clé minimum. Malheureusement, il peut y avoir jusqu'à n racines à vérifier. Dans cette seconde phase, on décroît donc le nombre de racines en connectant successivement les racines de même degré. Quand deux racines u et v ont le même degré, on met celle avec la plus grande clé des deux en fils de celle ayant la plus petite clé. Cette dernière voit son degré augmenter de un. On répète ceci jusqu'à ce que chaque racine ait un degré différent. Pour trouver efficacement les arbres de même degré, on utilise un tableau de longueur O(log n) dans lequel on garde un pointeur sur une racine de chaque degré. Quand on trouve une seconde racine avec le même degré, on connecte les deux et on met à jour le tableau. Le temps d'exécution réel est en O(log n + r), où r est le nombre de racines au début de la seconde phase. À la fin, on aura au plus O(log n) racines (parce que chacune a un degré différent). En conséquence, le potentiel décroît d'au moins r − O(log n) et le coût amorti est O(log n).

Dans la troisième phase, on regarde chacune des racines restantes et on trouve le minimum, ce qui est fait en O(log n) et n'entraîne pas de variation du potentiel. Le coût amorti total de l'extraction du minimum est donc O(log n).

Le tas de Fibonacci de la figure 1 après avoir diminué la clé du nœud 9 à 0. Ce nœud ainsi que ses deux ancêtres marqués sont coupés de l'arbre dont la racine est 1 et placés comme nouvelles racines.

L'opération diminuer clé va prendre le nœud, décroître sa clé, et si la propriété de tas est violée (la nouvelle clé est plus petite que la clé de son père), le nœud est coupé de son père. Si le père n'est pas une racine, il est marqué. S'il était déjà marqué, on le coupe aussi et son père est marqué. On continue comme ceci en remontant dans l'arbre jusqu'à ce qu'on atteigne soit la racine, soit un nœud non marqué. Ce faisant on crée un certain nombre, appelons le k, de nouveaux arbres. Chacun de ces nouveaux arbres, sauf peut-être le premier, était déjà marqué mais va perdre son marquage en devenant racine. Un seul nœud peut se retrouver marqué. Donc, le potentiel décroît d'au moins k − 2. Le temps d'exécution réel de la coupe est O(k), et donc le temps amorti est constant.

Finalement, l'opération supprimer peut être implémentée facilement en mettant la valeur de la clé de l'élément à supprimer à (la plus petite valeur représentable), de manière à ce qu'elle devienne la plus petite valeur du tas entier. Il suffit alors d'appeler extraire minimum pour le supprimer. Le coût amorti de cette opération est O(log n).