Tas de Fibonacci - Définition

Introduction

En informatique, un tas de Fibonacci est une structure de données similaire au tas binomial, mais avec un meilleur temps d'exécution amorti. Les tas de Fibonacci ont été conçus par Michael L. Fredman et Robert E. Tarjan en 1984 et publiés pour la première fois dans un journal scientifique en 1987. Les tas de Fibonacci sont utilisés pour améliorer le temps asymptotique de l'algorithme de Dijkstra, qui calcule les plus courts chemins dans un graphe, et de l'algorithme de Prim, qui calcule l'arbre couvrant de poids minimal d'un graphe.

Le nom de tas de Fibonacci vient des nombres de Fibonacci, qui sont utilisés pour calculer son temps d'exécution.

En particulier, les opérations insertion, trouver le minimum, décroître une clé, et union ont toutes un coût amorti constant. Les opérations supprimer et supprimer le minimum ont un coût amorti en O(log n). C'est-à-dire qu'en partant d'une structure vide, n'importe quelle séquence de a opérations du premier groupe et b opérations du second groupe prendrait un temps O(a + (b log n)). Dans un tas binomial, une telle séquence d'opérations prendrait un temps O((a + b)(log n)). Il devient donc plus intéressant d'utiliser un tas de Fibonacci plutôt qu'un tas binomial lorsque b est asymptotiquement plus petit que a.

Structure d'un tas de Fibonacci

Figure 1. Exemple de tas de Fibonacci à trois arbres de degrés 0, 1 et 3. Trois sommets sont marqués (en bleu). Le potentiel du tas est donc 9.

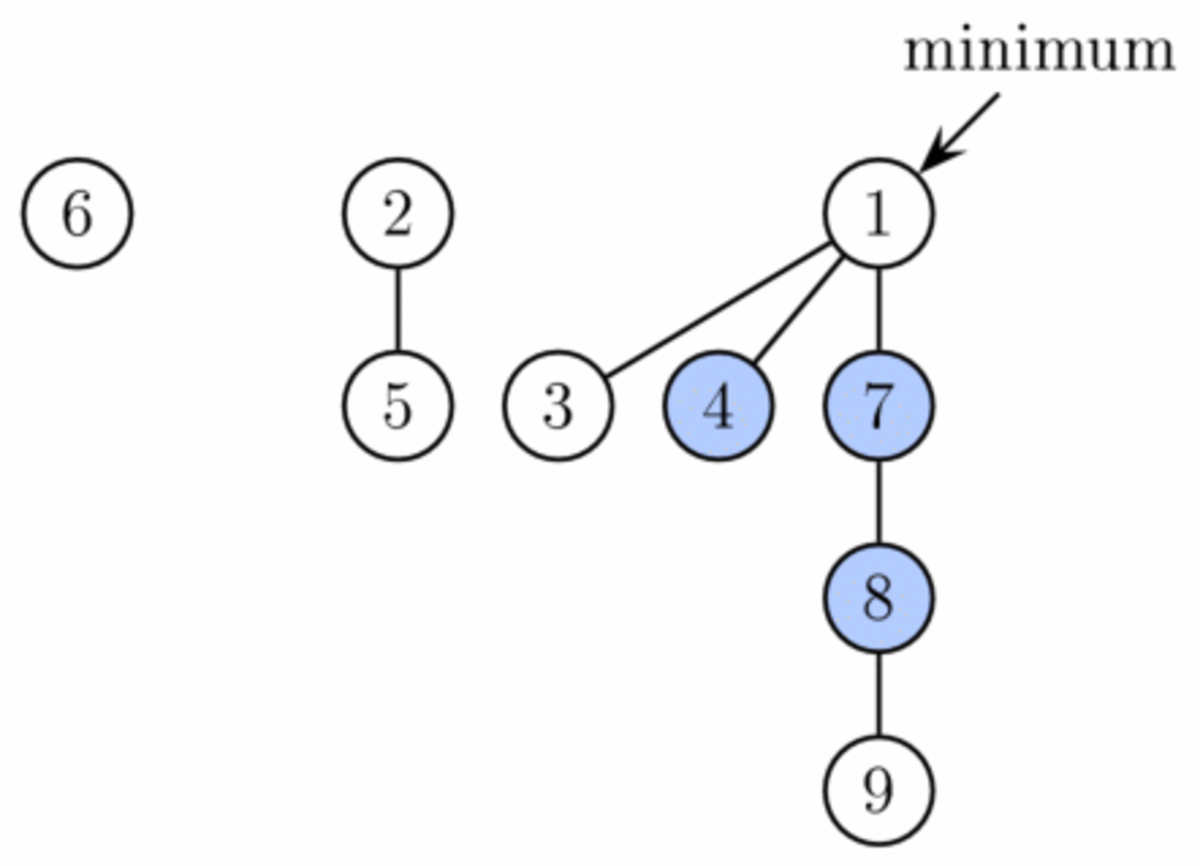
Un tas de Fibonacci est un ensemble d'arbres satisfaisant la propriété de tas-minimum, c'est-à-dire que la clé d'un fils est toujours supérieure ou égale à la clé de son père. Ceci implique que la clé minimum est toujours à la racine d'un des arbres. La structure des tas de Fibonacci est plus flexible que celle des tas binomiaux, en ce sens qu'elle permet à quelques opérations d'être exécutées de manière « paresseuse », en reportant le travail sur des opérations ultérieures. Par exemple, l'union de deux tas est effectuée simplement en concaténant les deux listes d'arbres, et l'opération de diminution de clé coupe parfois un nœud de son père pour former un nouvel arbre.

Cependant, à un moment donné il est nécessaire d'introduire un certain ordre dans la structure du tas de manière à obtenir le temps d'exécution voulu. En particulier, on garde les degrés des nœuds (c'est-à-dire leur nombre de fils) en dessous d'une valeur assez basse: chaque nœud a un degré au plus en O(log n) et la taille d'un sous-arbre d'un nœud de degré k est au moins F_k + 2, où F_k est le k^ème nombre de Fibonacci. Pour cela, on doit respecter la règle qui énonce qu'on ne peut couper au plus qu'un seul fils de chaque nœud non racine. Quand un second nœud est coupé, le nœud lui-même doit être coupé de son père pour devenir la racine d'un nouvel arbre. Le nombre d'arbres est diminué par l'opération supprimer le minimum, dans laquelle on relie les arbres.

En conséquence de cette structure flexible, certaines opérations peuvent prendre longtemps, alors que d'autres sont très rapides. En utilisant l'analyse amortie du temps d'exécution, on fait comme si les opérations très rapides prenaient un peu plus de temps qu'en réalité. On utilise ce temps « économisé » (comme dans un compte en banque) pour contrebalancer le temps réel d'exécution des opérations plus lentes. La quantité de temps économisé pour un usage ultérieur à un moment donné est mesurée par une fonction de potentiel. Le potentiel d'un tas de Fibonacci est donné par:

Potentiel = t + 2m

où t est le nombre d'arbres dans le tas de Fibonacci, et m est le nombre de nœuds marqués. Un nœud est marqué si au moins un de ses fils a été coupé depuis que ce nœud a été fait fils d'un autre nœud (aucune racine n'est marquée).

Ainsi, la racine de chaque arbre dans un tas possède une unité de temps en provision. Cette unité de temps peut être utilisée plus tard pour lier cet arbre avec un autre arbre en un coût amorti nul. Aussi, chaque nœud marqué a deux unités de temps en provision. Une unité peut être utilisée pour couper le nœud de son père. Quand c'est le cas, le nœud devient une racine et la deuxième unité de temps reste en stock dans ce nœud comme dans chaque racine.