Théorème de Ceva - Définition

Exemples d'application

Le théorème de Ceva permet de démontrer de nombreuses propriétés de droites concourantes.

• On peut l'appliquer à un cas simple comme le point d'intersection des médianes. Dans ce cas, D est le milieu de [BC] et donc . De même pour les autres points. Tous les rapports intervenant dans le théorème valent 1, et donc leur produit aussi, ce qui prouve que les médianes d'un triangle sont concourantes.

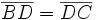
• Les conjugués isogonaux sont un autre exemple d'application du théorème de Ceva.