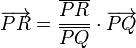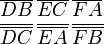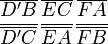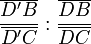Théorème de Ceva - Définition

Géométrie affine

Il s'avère que le théorème de Ceva (la première version), est un énoncé de géométrie affine, c'est-à-dire qu'il n'est pas besoin de parler de longueur, d'orthogonalité, ou d'angle, même si bien sûr le théorème reste valide a fortiori dans ce contexte. Pour cela on doit abandonner les longueurs et donner un énoncé en termes de rapports de mesures algébriques. Une mesure algébrique est intuitivement, en géométrie euclidienne, une longueur avec un signe qui dépend d'une orientation arbitraire sur une droite donnée. Mais on peut définir de façon purement affine, sans parler ni de longueur, ni d'orientation, le rapport de mesures algébriques suivant pour trois points P, Q, R alignés, Q et R étant distincts de P, soit :

.

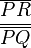
Il s'agit du rapport de la seule homothétie de centre P qui transforme Q en R, ou encore de façon équivalente, du seul scalaire vérifiant :

L'énoncé du théorème qui suit est donc bien un énoncé de géométrie affine.

Le théorème

Théorème — Soit ABC un triangle, soient D, E et F trois points distincts des sommets et appartenant respectivement aux droites (BC), (CA) et (AB). Les droites (AD), (BE) et (CF) sont concourantes ou parallèles si et seulement si

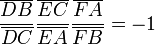
Démonstration : Il existe de nombreuses démonstrations du théorème de Ceva en géométrie affine. Plutôt que d'adapter la démonstration précédente, ce qui demanderait d'introduire une notion d'aire algébrique on va utiliser directement le barycentre, et faire appel aux propriétés suivantes.

• Si M est barycentre de distinct de A et B alors .
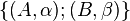
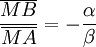
• Soit M le barycentre de , M non situé sur [AB], [BC] ou [CA]. (AM) rencontre (BC) en D si et seulement si .

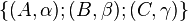
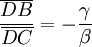
La démonstration se fait en trois temps.

Si les droites (AD), (BE), (CF) sont parallèles alors le produit des trois rapports est -1

L'application du théorème de Thalès d'une part dans le triangle (CBE), avec (DA) parallèle à (BE), d'autre part dans le triangle (BCF), avec (DA) parallèle à (CF) conduit à dire que :

    et    

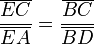
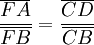
Il suffit alors de remplacer pour montrer que le produit des trois rapports est égal à -1.

Si les droites sont concourantes alors le produit des trois rapports est -1

On note M le point de concours. Il est situé ni sur [AB], ni sur [BC], ni sur [CA]. Il est barycentre de

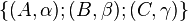
(AM) rencontre (BC) en D donc .

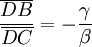
Par un raisonnement analogue, on obtient aussi et

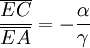
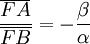
Le produit des trois rapports est alors bien égal à -1.

Si le produit des trois rapports est -1 alors les droites sont parallèles ou concourantes

Si les trois droites sont parallèles, il n'y a rien à démontrer.

Dans le cas contraire, deux au moins sont sécantes, on peut sans perdre de généralité, supposer que ce sont les droites (AD) et (BE) sécantes en M non situé sur [AB], [BC] ou [CA] et barycentre de

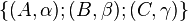
Comme (AM) rencontre (BC) en D et que (BM) rencontre (CA) en E, on peut écrire et

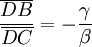
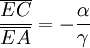
Enfin, on a

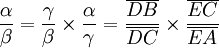
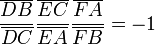
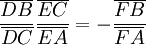
Or donc

Donc ce qui assure que la droite (CM) coupe bien la droite (AB) en F.

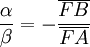
Les trois droites sont bien concourantes en M.

On observe une parenté formelle entre cette démonstration et celle par les aires : M est barycentre des points A, B et C en prenant pour coefficients les aires des trois triangles MAB, MBC et MCA de la première démonstration.

Théorème de Ceva et théorème de Ménélaüs

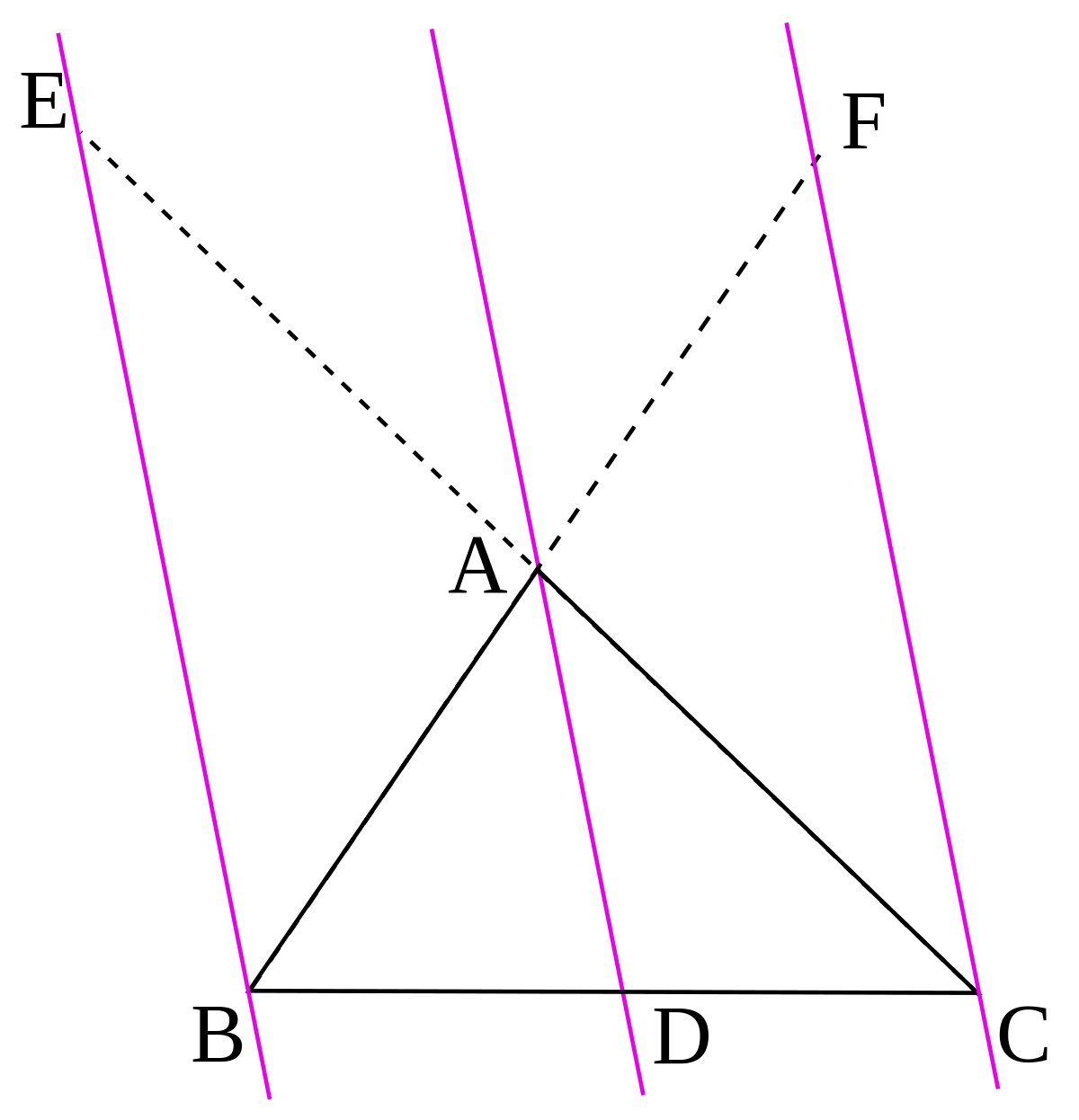
Le théorème de Ceva entretient des rapports étroits avec le théorème de Ménélaüs qui donne une condition très analogue (le même produit doit égaler 1), pour que trois points sur les côtés (en tant que droites) d'un triangle soient alignés.

La configuration du théorème de Ménélaüs est en effet duale de celle du théorème de Ceva : la dualité fait correspondre point et droite et prend tout son sens en géométrie projective, le dual d'un triangle est un triangle dont on a échangé les sommets et les côtés. Les points duaux des céviennes (passant par les sommets) sont des points sur les côtés du triangle dual. La condition de concourance des céviennes devient une condition d'alignement de ces points.

D'autre part on montre le théorème de Ceva en utilisant deux fois le théorème de Ménélaüs. Il s'agit de l'une des implications de l'équivalence du théorème, et on suppose de plus que les trois droites concourantes. Avec les mêmes notations que ci-dessus, on applique le théorème de Ménélaüs aux triangles ABD, avec les trois points incidents aux côtés F, M et C et au triangle ADC avec B, M et E, et on obtient le théorème de Ceva par quotient.

Du théorème de Ceva au théorème de Ménélaüs et réciproquement par la division harmonique .

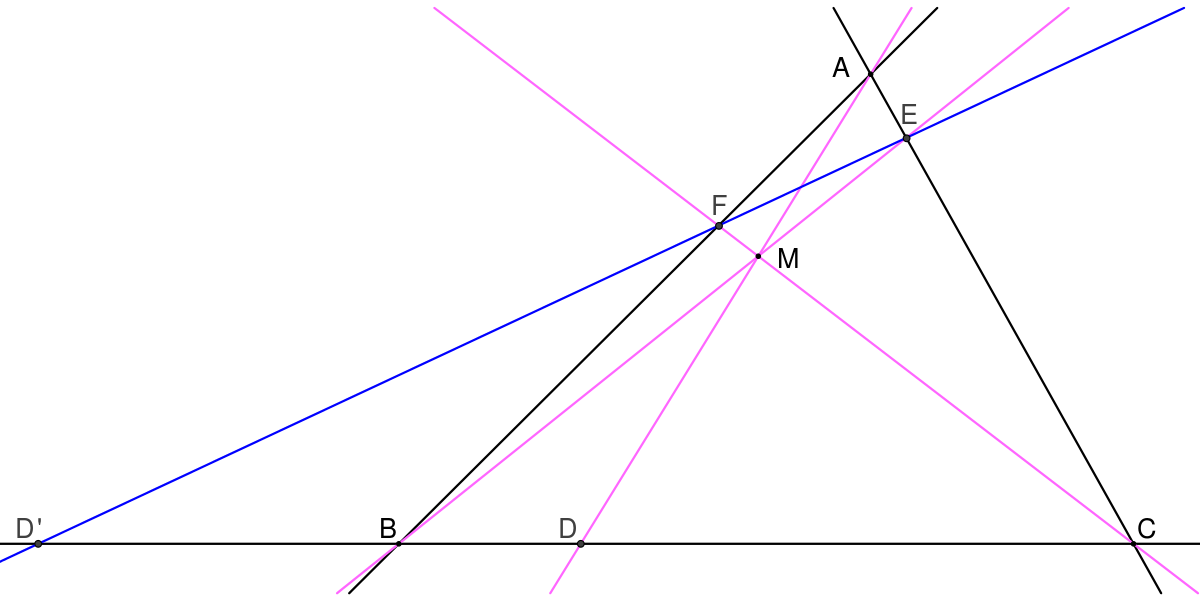
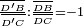
Enfin on passe du théorème de Ceva au théorème de Menelaüs par une division harmonique. Dans le triangle ABC, les points D, E et F sont sur les côtés respectivement (BC), (AC) et (AB), tels que les droites (AD), (CF) et (BE) soient concourantes et la droite (FG) ne soit pas parallèle au côté (BC), le point D’ est alors l'intersection de ces deux droites, c'est-à-dire que D’ est sur (BC) et D’, F et G sont alignés ; alors les quatre points [D’,D,B,C] sont en division harmonique :

		− 1		Ceva
		1		Ménélaüs
		− 1		(AD) est la polaire de D’ par rapport à (AB) et (AC)

On passe, par un simple produit ou quotient, de deux de ces résultats au troisième (voir l'article division harmonique pour la définition de la polaire et une démonstration de la propriété utilisée, c'est celle qui permet de construire la polaire, utilisant les faisceaux harmoniques). Une autre façon de mettre en évidence cette propriété est de remarquer que les quatre droites (AB), (BE), (CF) et (CA) sont les côtés d'un quadrilatère complet de sommets A, F, M, E, B et C : la diagonale [BC] est donc divisée par les deux diagonales (EF) et (AM) suivant une division harmonique.