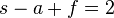Théorème de Descartes-Euler - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
La version de Descartes
Dans son mémoire inédit, Descartes énonce le théorème suivant :
«L'angle droit étant pris pour unité, la somme des angles de toutes les faces d'un polyèdre convexe est égale à quatre fois le nombre de sommets diminué de 2
»
L'aspect du théorème semble fort éloigné de la relation d'Euler. Elle lui est pourtant rigoureusement équivalente et Descartes dans les applications qu'il en fait passe assez naturellement de cette forme à celle d'Euler.
Preuve de l'équivalence :
- Il faut se servir de la propriété de la somme des angles d'un polygone convexe : si le polygone convexe a n côtés, la somme des angles vaut 2(n - 2) droits.
- La somme de tous les angles sur toutes les faces est donc
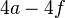
- L'égalité de Descartes s'écrit donc
-
- Rigoureusement équivalente à
-