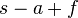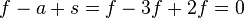Théorème de Descartes-Euler - Définition

Applications

• Il est impossible de recouvrir une sphère seulement par des hexagones, même non réguliers, afin de former une géode, car un tel recouvrement ne respecterait pas la relation d'Euler. En effet, dans un polyèdre à faces uniquement hexagonales, chaque sommet est commun à 3 faces et chaque arête à 2 faces. Comme tout hexagone a 6 côtés et 6 sommets, un tel polyèdre doit donc comporter plus de sommets que de faces et plus d'arêtes que de faces. Donc, si f est le nombre de faces, le nombre d'arêtes a doit être égal à 3f et le nombre de sommets s à 2f. On a alors :

et la relation d'Euler n'est pas vérifiée.

Par contre, remplaçons certains hexagones de ce recouvrement impossible par des pentagones. Si le nombre de faces ne varie pas, le nombre d'arêtes et de sommets diminue : pour chaque pentagone ajouté, on a ( 6 - 5 )÷ 2 arêtes, c'est-à-dire une demi-arête en moins et (6 - 5)÷3 sommets, c'est-à-dire un tiers de sommet en moins;   s − a + f   augmente donc à chaque fois de la différence, c'est-à-dire d'un sixième. Pour que la relation d'Euler soit respectée, il faut que   s − a + f   initialement à 0, devienne égal à 2, donc augmente de 12÷6. Bref, il faut remplacer 12 hexagones par autant de pentagones. Le nombre des sommets s est alors de 2f - 4 et celui des arêtes a de 3f - 6. C'est ainsi que l'on rencontre l'icosaèdre tronqué (ballon de football ou fullerène C₆₀). Un cas extrême est celui du dodécaèdre ( f = 12 ), où il ne reste plus aucun hexagone. Dans la figure ci-dessous (où f = 344 faces), quatre des douze pentagones sont visibles.

géode duale

Lien avec les pavages de la sphère

On peut ramener cette relation à une propriété de pavage de la sphère, en utilisant la technique imagée suivante

• placer une source de lumière au centre de gravité G du polyèdre
• considérer une sphère de centre G et de rayon suffisamment grand, et la considérer comme un écran sur lequel se projettent les ombres des arêtes du polyèdre.

Cette opération est en fait une projection centrale. On obtient alors sur la sphère des «sommets», images des sommets du polyèdre, des «arêtes» qui sont des arcs de grands cercles, et des portions de sphères délimitées par les arêtes qui sont des «polygones sphériques». On peut qualifier cette configuration de pavage de la sphère par des polygones sphériques.

On montre encore que pour un tel pavage, la formule F + S - A = 2 est vérifiée. Une des méthodes possibles est d'utiliser des propriétés des triangles sphériques.

Généralisations

Henri Poincaré, en 1893 a démontré que la relation d'Euler se généralisait à tout n-polytope convexe :

N₀ − N₁ + N₂ − N₃ + ... + ( − 1)^{n − 1}N_{n − 1} = 1 − ( − 1)ⁿ

où n est la dimension du polytope et N_k le nombre de k-simplexes du n-polytope (N₀ est le nombre de sommets, N₁ le nombre d'arêtes, N₂ le nombre de faces etc. )

La quantité ., si elle vaut 2 dans le cas des polyèdres de genre 0, peut prendre d'autres valeurs suivant la nature du polyèdre et est appelée caractéristique d'Euler (ou d'Euler-Poincaré) du solide. Cette caractéristique est un nombre qu'on peut attacher naturellement aux surfaces. Elle est par exemple de 2 pour la sphère. Il s'agit d'un invariant topologique, c'est-à-dire que toutes les variétés homéomorphes à la sphère ont la même caractéristique. La convexité n'est finalement qu'une hypothèse particulière assurant qu'il existe bien un tel homéomorphisme.