Théorème de Descartes-Euler - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le théorème de Descartes-Euler (ou relation d'Euler), formulé par Leonhard Euler en 1752, énonce une formule mathématique qui relie le nombre de côtés, de sommets, et de faces dans un polyèdre du genre 0. Un polyèdre de genre 0 est un polyèdre sans trou : en supprimant une face on obtient une surface simplement connexe ; un polyèdre convexe est de genre 0.
Il semble cependant que Descartes ait prouvé une relation analogue dans un traité jamais publié. C'est la raison pour laquelle cette relation porte ce double nom.
Énoncé
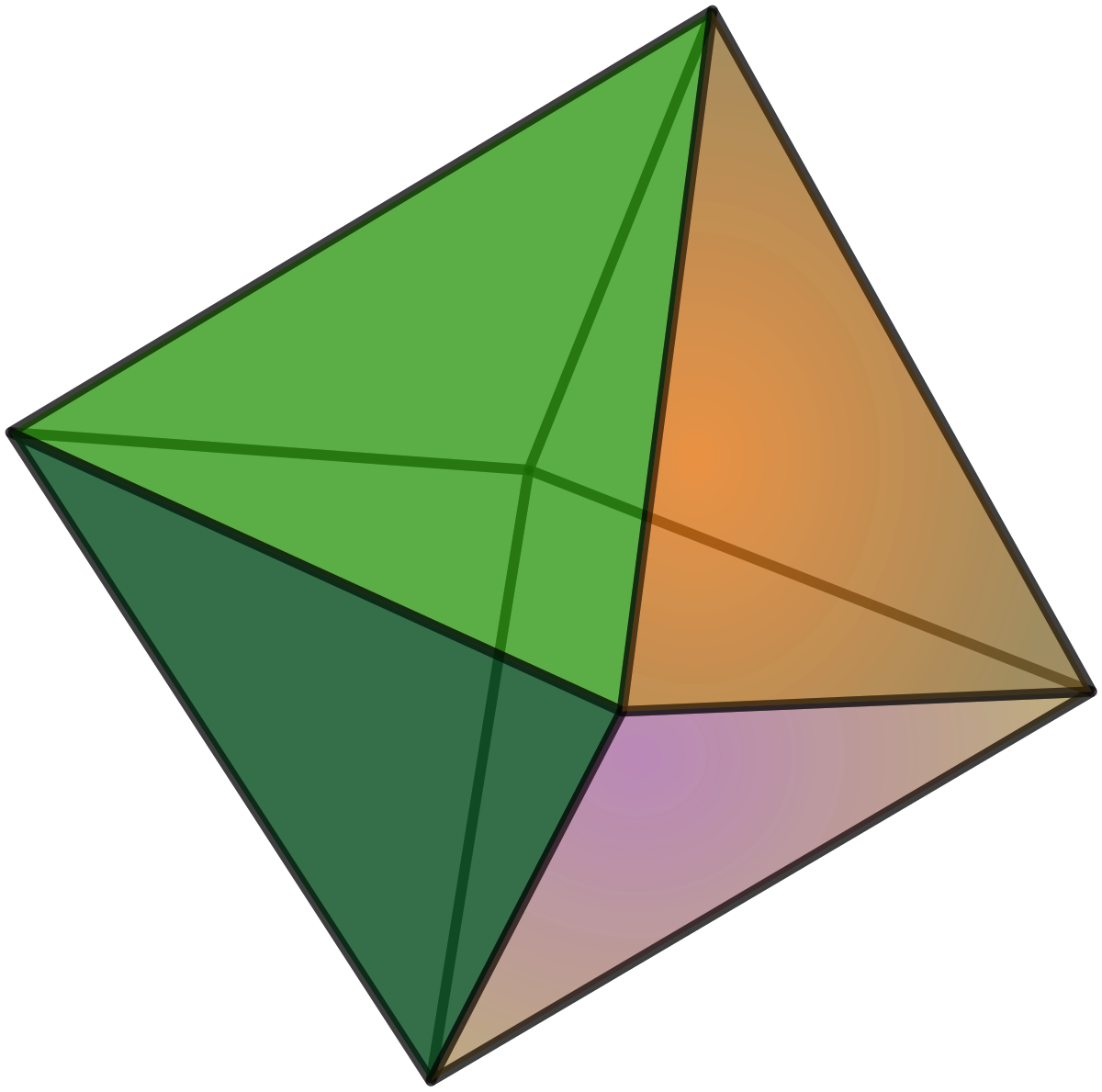
Soit un polyèdre de genre 0, on note :
- f le nombre de faces de celui-ci,
- a le nombre d'arêtes de celui-ci,
- s le nombre de sommets de celui-ci,
On peut démontrer qu'on a toujours :
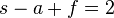
Preuve
La preuve présentée ici est la première démonstration rigoureuse de la relation d'Euler. Elle a été donnée par Cauchy, alors âgé de 20 ans :
Soit un polyèdre de genre 0, on va chercher à démontrer que
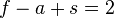
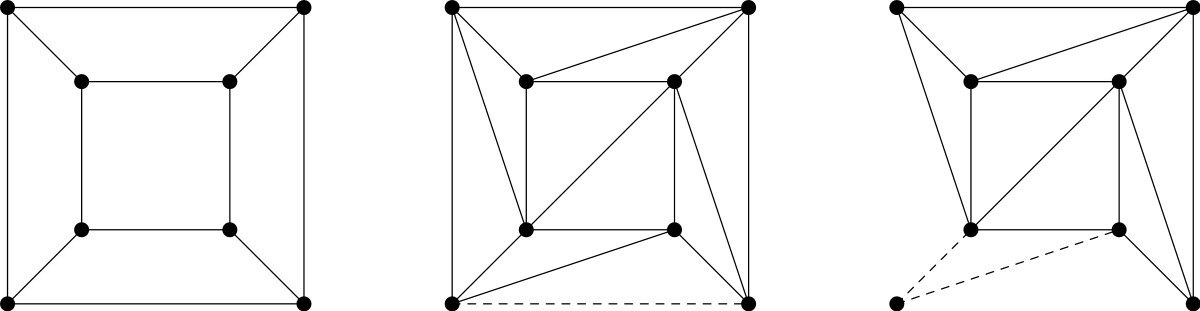
Maintenant, à chaque fois qu'on voit une face ayant plus de trois côtés, on trace une diagonale (c’est-à-dire un arc joignant deux sommets non directement reliés). Cette opération ajoute une face et une arête à notre graphe et ne modifie pas le nombre de sommets, donc l'expression
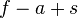
Arrivé à ce stade, on répète les deux opérations suivantes :
- On supprime un à un tous les triangles qui comportent 'un' seul côté aux frontières extérieures de notre graphe. A chaque suppression, on enlève une arête et une face (pas de modification au niveau des sommets). Cela conserve donc l'expression
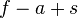
- On supprime un à un tous les triangles qui comportent 'deux' arêtes aux frontières extérieures de notre graphe. A chaque suppression, on enlève un sommet, deux arêtes et une face. Cela conserve donc à nouveau l'expression
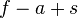
En répétant les deux étapes précédentes, l'une après l'autre, il ne finit par rester qu'un seul triangle. Ce triangle seul compte deux faces (l'intérieur et l'extérieur du triangle), trois arêtes et trois sommets. Ainsi f = 2, a = 3, et s = 3, donc
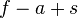
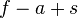
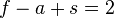
Exemples et contre-exemples
On peut procéder à la vérification de la propriété pour les cinq solides platoniciens
| Nom | Image | S (sommets) | A (arêtes) | F (faces) | Caractéristique d'Euler : S − A + F |
|---|---|---|---|---|---|
| Tétraèdre |
| 4 | 6 | 4 | 2 |
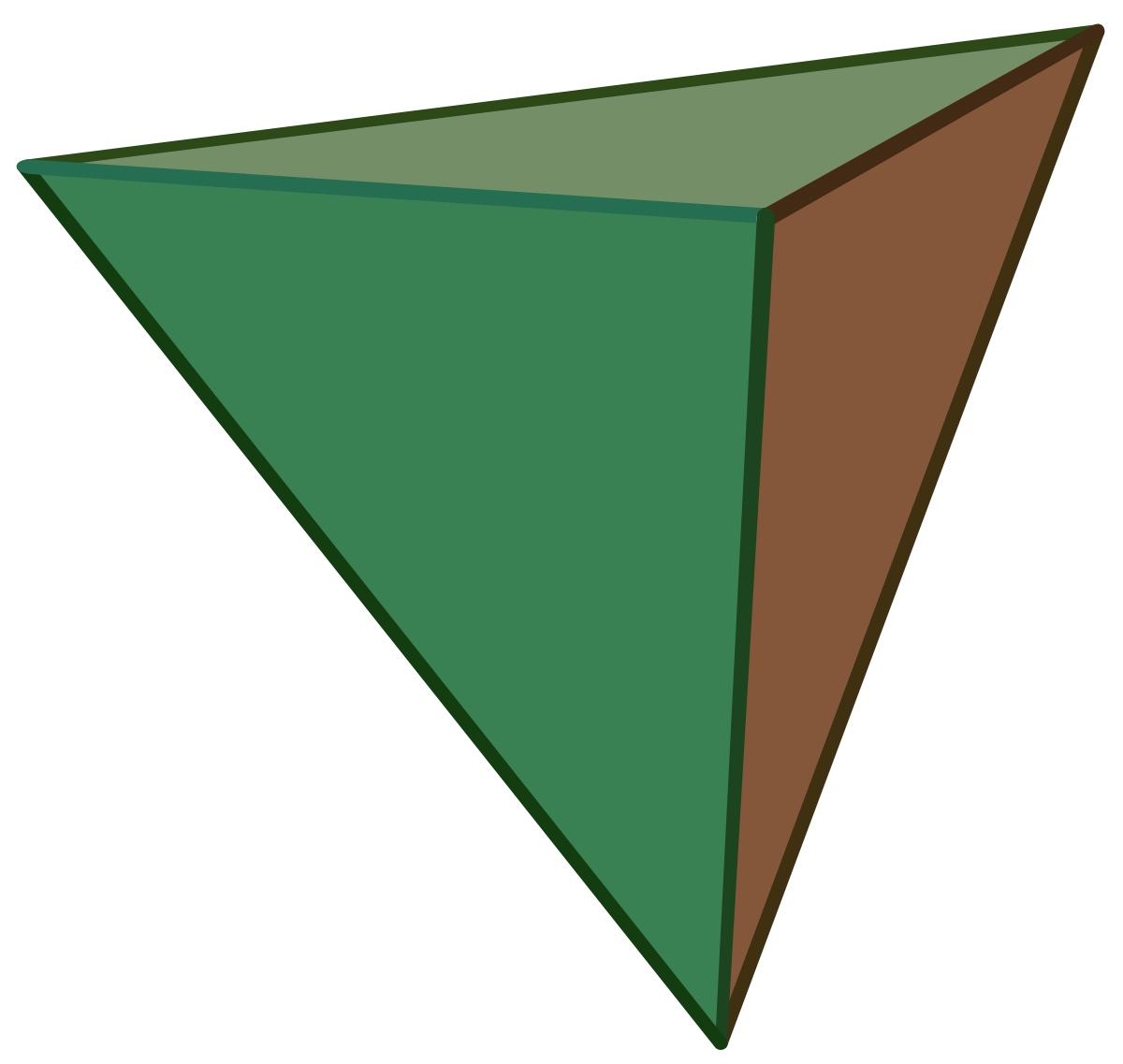
| Hexaèdre ou cube |
| 8 | 12 | 6 | 2 |
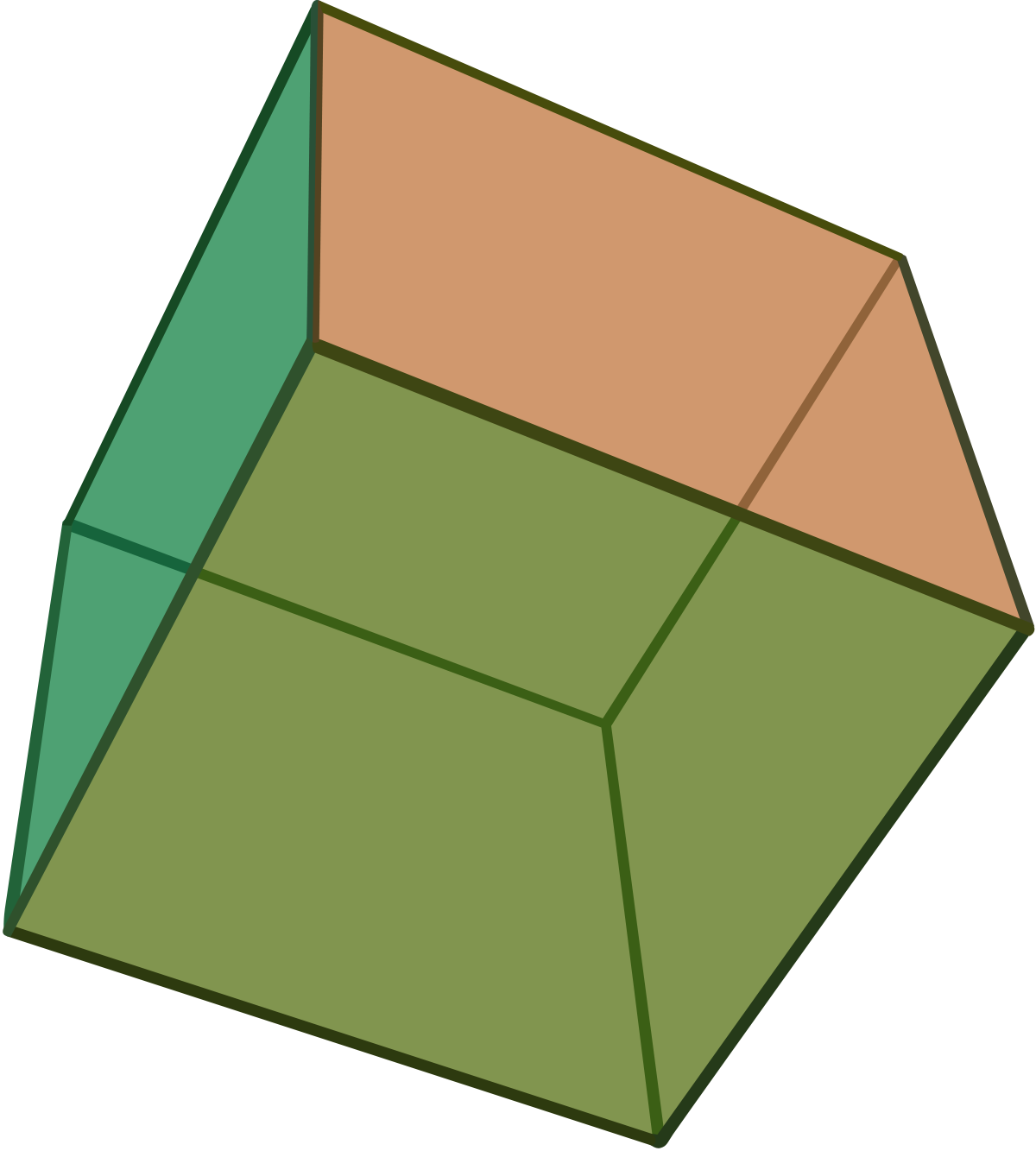
| Octaèdre |
| 6 | 12 | 8 | 2 |
| Dodécaèdre | 20 | 30 | 12 | 2 | |
| Icosaèdre |
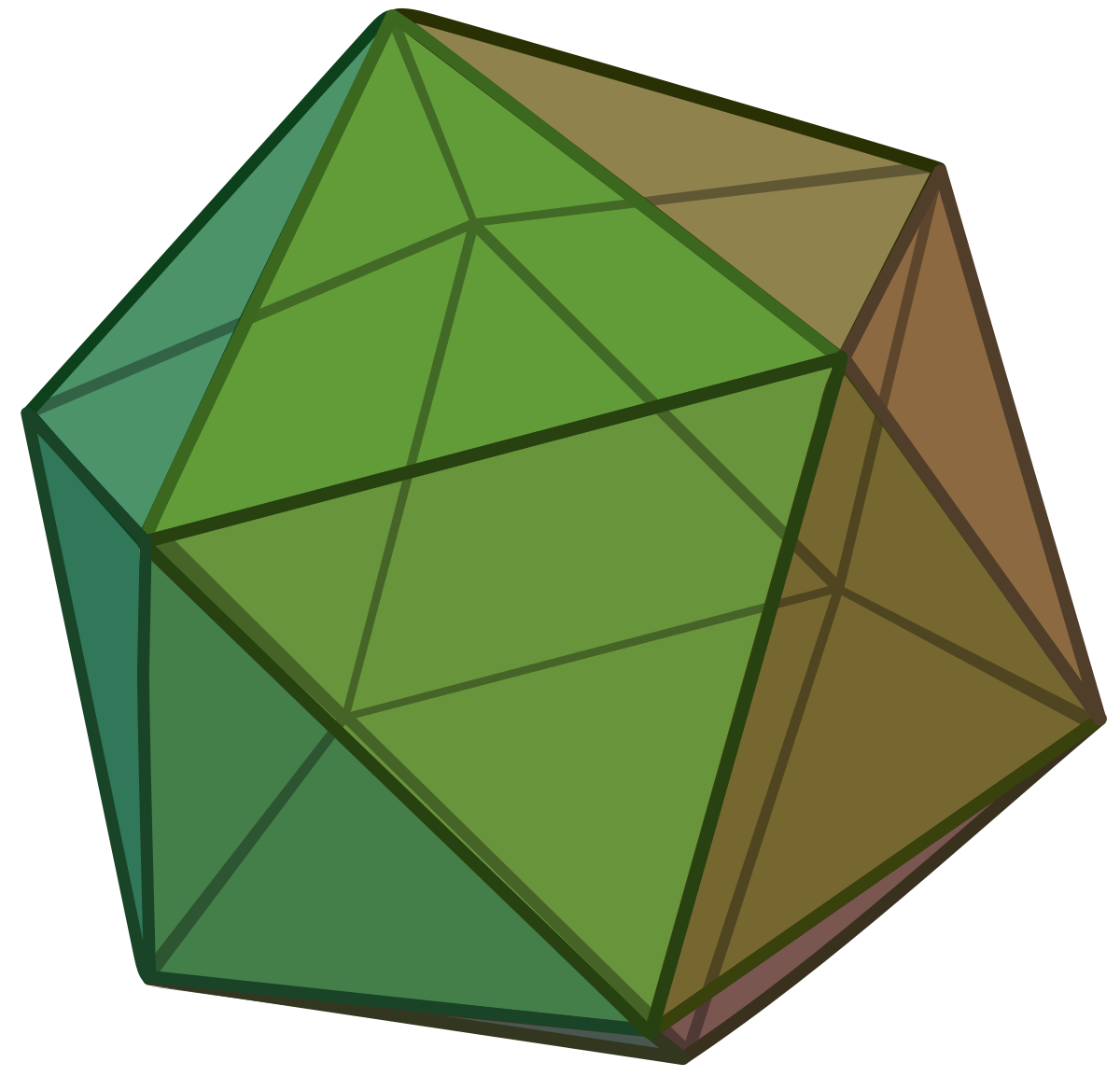
| 12 | 30 | 20 | 2 |
Si les polyèdres ne sont pas convexes, ils ne sont pas du genre 0 et on ne peut pas appliquer le théorème de Descartes-Euler. On peut alors trouver pour S − A + F des valeurs différentes de 2:
| Nom | Image | S (Sommets) | A (arêtes) | F (faces) | Caractéristique d'Euler : S − A + F |
|---|---|---|---|---|---|
| Tetrahemihexaèdre |
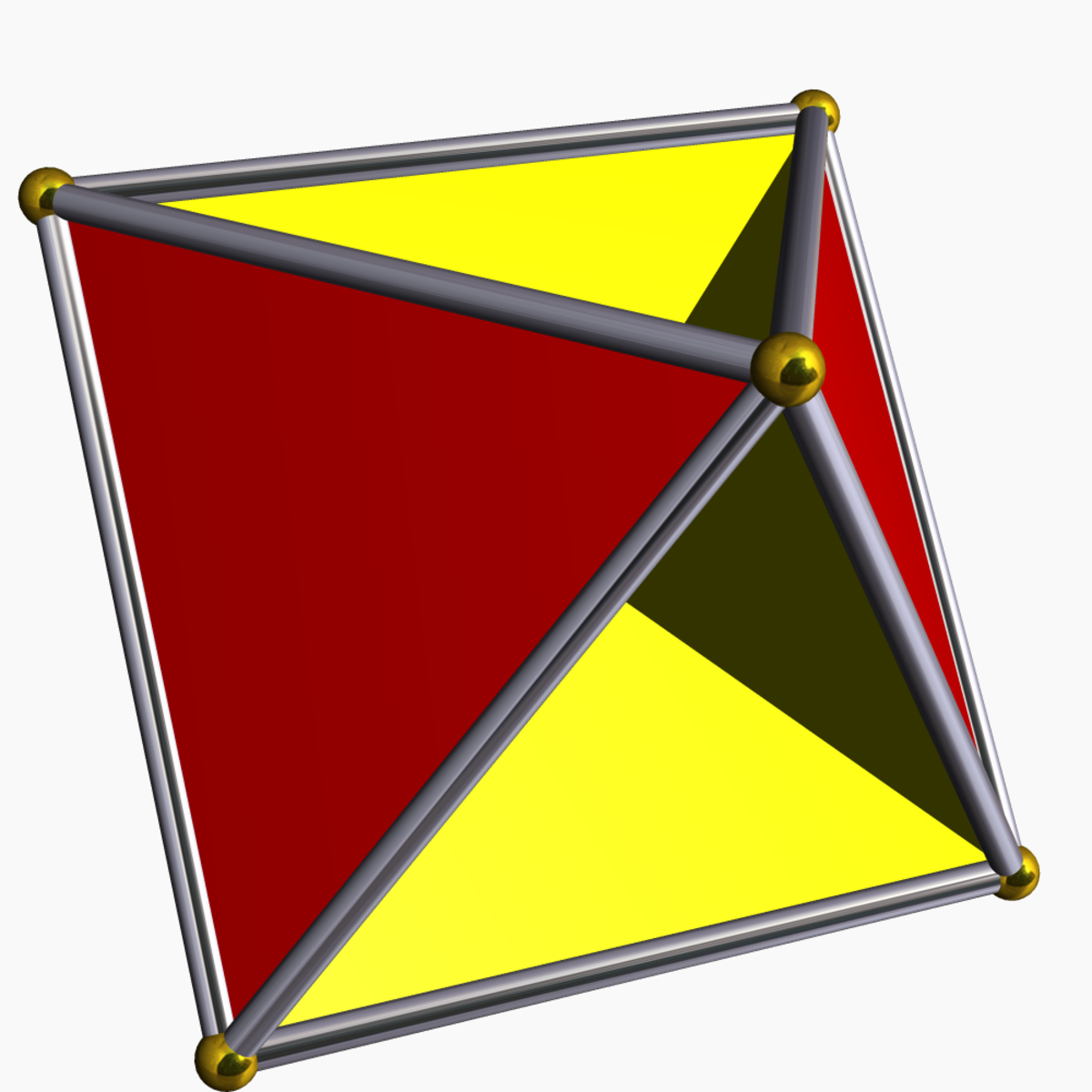
| 6 | 12 | 7 | 1 |
| Octahemioctaèdre |
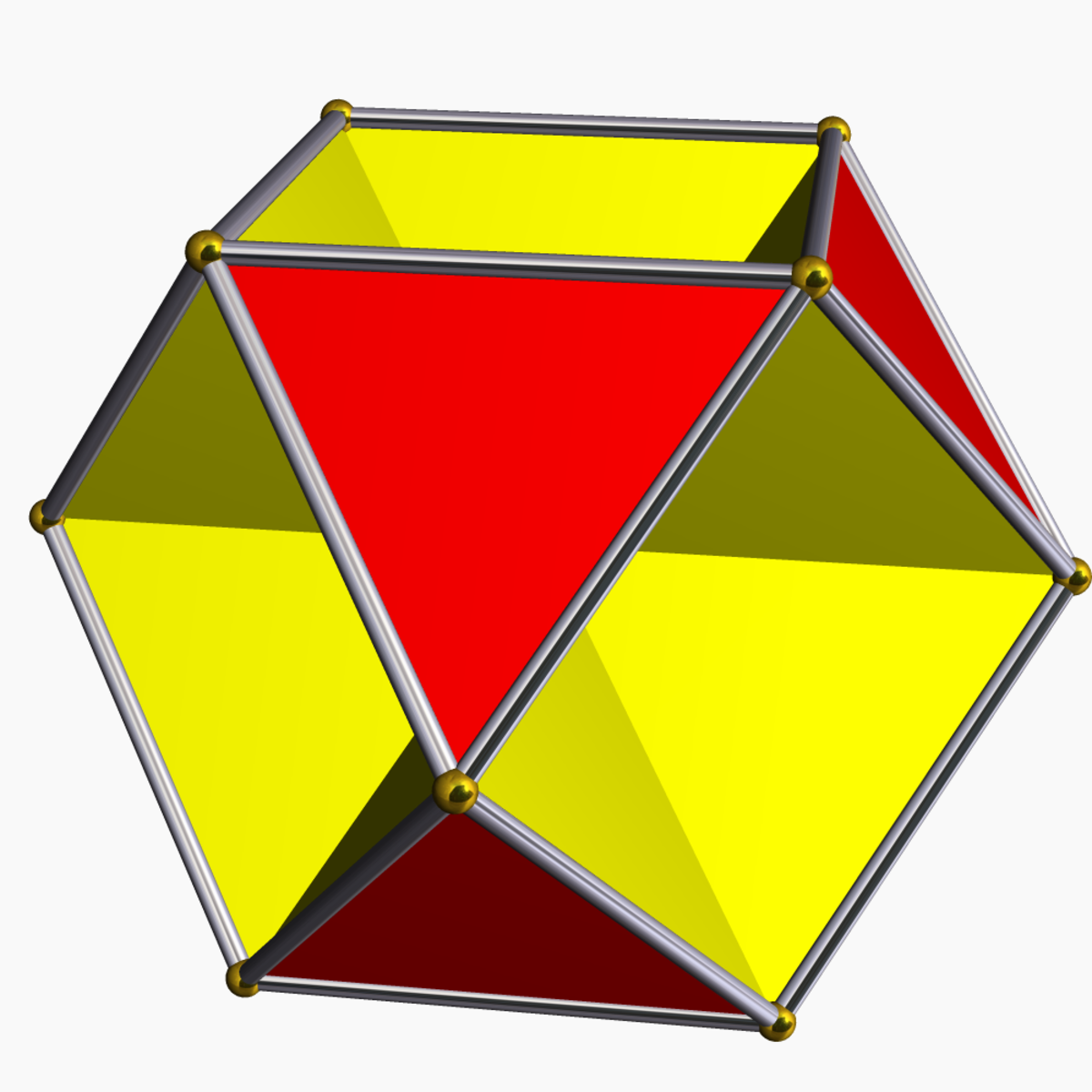
| 12 | 24 | 12 | 0 |
| Cubohemioctaèdre |
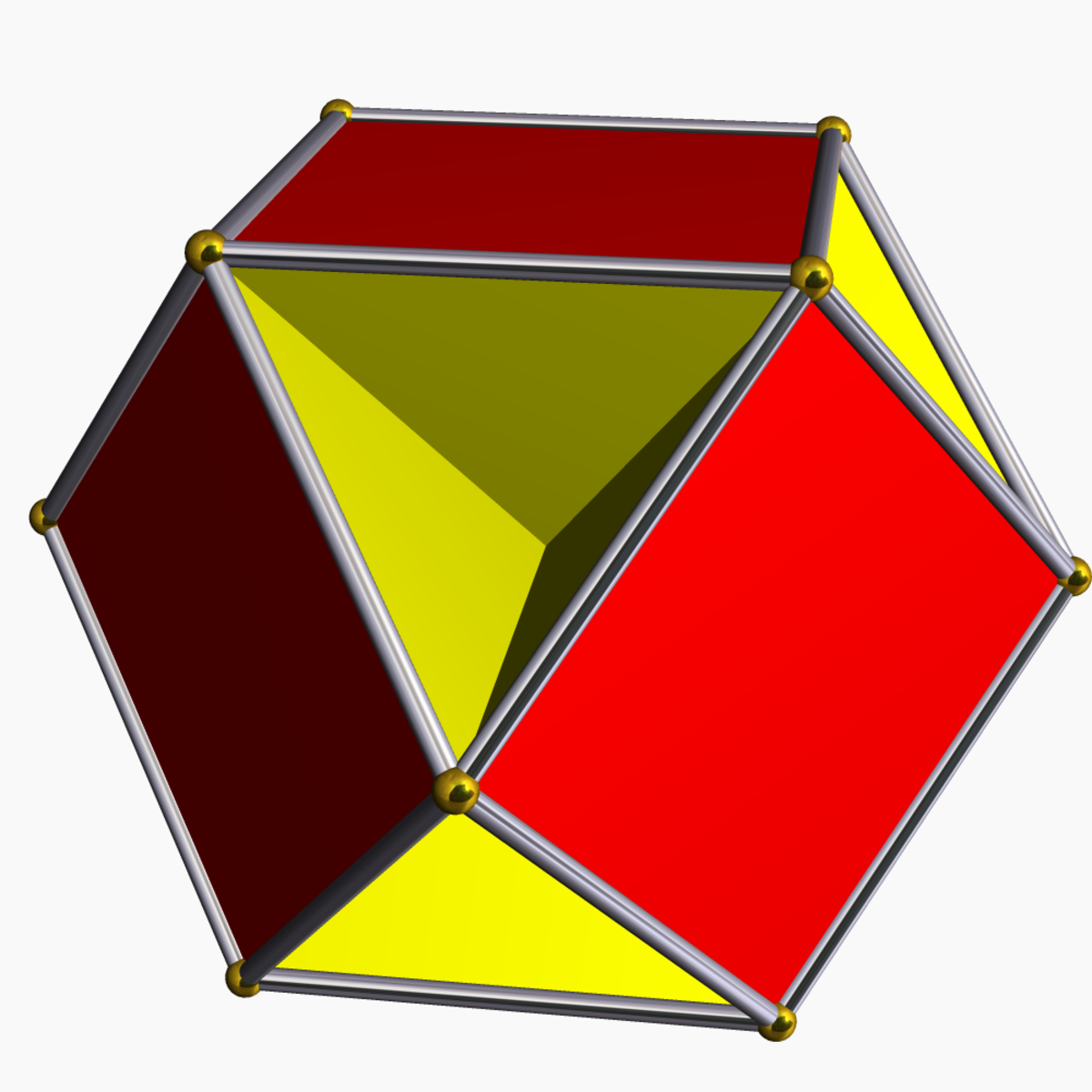
| 12 | 24 | 10 | −2 |

















































