Théorèmes de l'alternative - Définition
La liste des auteurs de cet article est disponible ici.
Les théorèmes de l'alternative : point de vue matriciel
Pour B matrice réelle, la notation
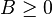
Traductions matricielles des énoncés déjà donnés
Commençons par la version matricielle du lemme de Farkas, puisque c'est le théorème le plus notable. Elle s'obtient sans aucune subtilité à partir de la version donnée plus haut, la seule difficulté étant de bien rapprocher les notations de l'une et de l'autre.
Lemme de Farkas, version matricielle — Soit A une matrice de réels de type (n,k) et b un vecteur-colonne avec n entrées, alors un et un seul des systèmes linéaires suivants a une solution :
- le système
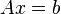
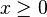
- ou le système
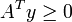
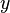
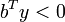
La vérification qui suit utilise les notations non de la version donnée plus haut mais de la version dite « version vectorielle » dans l'article lemme de Farkas (qui lui est équivalente de façon immédiate) à laquelle on se réfèrera donc.
Pour chaque colonne Cj de A (
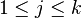

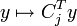
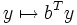
L'existence d'une solution pour la première branche de l'alternative, c'est l'existence d'un k-uplet
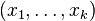
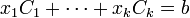
L'existence d'une solution pour la deuxième branche de l'alternative, c'est l'existence d'un y qui soit dans
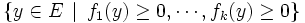
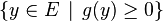
L'équivalence annoncée par le théorème de Farkas garantit donc précisément qu'un et un seul des deux systèmes a une solution.
On écrit de même des versions matricielles pour les théorèmes de Gordan et de Stiemke, dont la vérification est du même esprit.
Théorème de Gordan, version matricielle — Soit A une matrice de réels de type (n,k). Alors un et un seul des systèmes linéaires suivants a une solution :
- le système
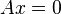
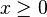
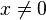
- ou le système ATy > 0 pour
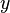
Théorème de Stiemke, version matricielle — Soit A une matrice de réels de type (n,k) et b un vecteur-colonne avec n entrées, alors un et un seul des systèmes linéaires suivants a une solution :
- le système
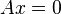
- ou le système
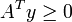
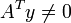
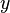
Le théorème de Ville
Ce théorème de Jean Ville, qui se déduit en quelques lignes du théorème de Gordan dès lors qu'on manipule les notations matricielles, a un énoncé très agréablement symétrique sous cette forme ; on peut bien sûr le réécrire en termes de conditions nécessaire et suffisante d'existence de solutions de systèmes d'inéquations, son charme étant qu'on peut le faire de deux façons selon l'ordre dans lequel on considère les deux branches de l'alternative : au choix on peut y voir une condition nécessaire et suffisante d'existence de solutions en nombres positifs ou nuls pour un système d'inégalités linéaires larges, ou d'existence de solutions en nombres strictement positifs pour un système d'inégalités linéaires strictes.
Théorème de Ville (1938) — Soit A une matrice de réels de type (n,k). Alors un et un seul des systèmes linéaires suivants a une solution :
- le système
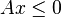

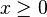
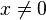
- ou le système
 pour y vecteur-colonne à n entrées vérifiant par ailleurs y > 0.
pour y vecteur-colonne à n entrées vérifiant par ailleurs y > 0.
Il se vérifie en quelques lignes : introduisons la matrice définie par collage de deux blocs :
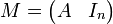
La deuxième branche est immédiate : MTy > 0 est directement équivalent à ATy > 0 et y > 0, ce qui est exactement le système figurant en deuxième branche de l'alternative dans l'énoncé qu'on est en train de montrer.
La première demande un peu plus de concentration. L'existence d'un z tel que Mz = 0 avec
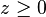
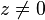
- Ax + v = 0,
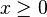
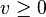
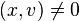
Ce système équivaut immédiatement à :
- Ax + v = 0,
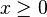
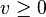
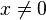
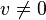
Enfin on s'aperçoit que ce dernier système a des solutions, si et seulement si, le système plus simple, de seule inconnue x :
-
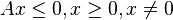
On reconnaît la première branche de l'alternative dans l'énoncé du théorème de Ville, qui est ainsi prouvé.

















































