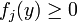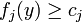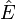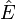Théorèmes de l'alternative - Définition
La liste des auteurs de cet article est disponible ici.
Systèmes mêlant inéquations strictes et larges : le lemme de Farkas et le théorème de Motzkin
Les énoncés
Le lemme de Farkas énonce une condition nécessaire et suffisante d'inconsistance pour un système d'inéquations linéaires dont exactement une est stricte :
Lemme de Farkas (1902) — Soit
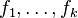
si et seulement si
- il existe une écriture
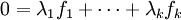
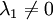
Enfin le théorème de Motzkin couvre le cas général d'un système mélant inéquations strictes et inéquations larges, avec une au moins stricte ; le lemme de Farkas en est le cas particulier correspondant à p = 1 (le théorème de Gordan correspondant à p = n) :
Théorème de Motzkin (1936) — Soit
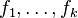
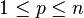
si et seulement si
- il existe une écriture
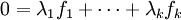
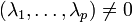
Le théorème de Gordan entraîne le lemme de Farkas
Le théorème de Gordan se démontre en moins d'une dizaine de lignes à condition de disposer des théorèmes de séparation des convexes ou de projection sur un convexe fermé. On peut à partir de là prouver le lemme de Farkas avec un peu de gymnastique supplémentaire, qui ne nécessite aucun outil avancé mais n'est pas complètement naturelle.
On montre le lemme de Farkas par récurrence sur la dimension. Il est évident en dimension 0 ou 1 ; supposons le vrai en toute dimension strictement inférieure à
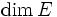
On vérifie sans mal que si on dispose du théorème de Farkas pour des familles de formes linéaires toutes non nulles, les cas particuliers où telle ou telle des fj est la forme nulle s'en déduit sans aucune difficulté. On supposera dès lors toutes les fj non nulles.
Supposons inconsistant le système qui apparaît dans l'énoncé du lemme de Farkas. Celui qui apparaît dans l'énoncé de Gordan est a fortiori inconsistant. On peut donc écrire :
avec des réels positifs ou nuls λj dont un au moins n'est pas nul.
- Cas évident : si
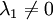
- Cas problématique : si λ1 = 0. Quitte à renuméroter les fj, on peut alors supposer qu'il y a un
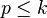

-
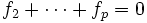
Notons
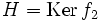
 est sans solution dans H.
est sans solution dans H.
Il existe donc des réels positifs ou nuls
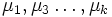
- pour tout y de H,
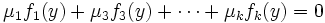
Les formes linéaires nulles sur l'hyperplan
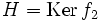
-

-
- Si
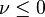
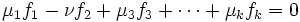
- Si
-
- Si ν > 0, on récupère la relation en attente
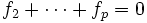
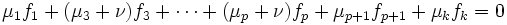
- Si ν > 0, on récupère la relation en attente
Le lemme de Farkas entraîne le théorème de Motzkin
Bien que le théorème de Motzkin semble plus général que celui de Farkas, il s'en déduit en quelques lignes, comme suit :
On note, pour des indices variant de 1 à p :
On remarque que si on prend y1 dans C1, y2 dans C2,
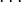
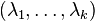
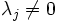
Comme dans tous les théorèmes rassemblés ici, l'implication montante est une évidence.
Extension à des systèmes d'inéquations affines
Une fois connus ces théorèmes, on peut en déduire en tant que de besoin des énoncés pour des systèmes affines, c'est-à-dire où les inéquations n'auraient pas la forme