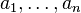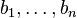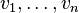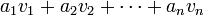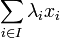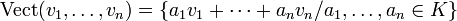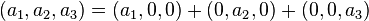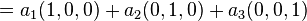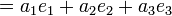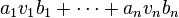Combinaison linéaire - Définition

Introduction

En mathématiques, les combinaisons linéaires sont un concept central de l'algèbre linéaire et d'autres domaines des mathématiques connexes. La majeure partie de cet article traite des combinaisons linéaires dans le contexte d'espace vectoriel sur un corps commutatif, et indique quelques généralisations à la fin de l'article.

Définitions

Supposons que K soit un corps commutatif et E un espace vectoriel sur K. Comme d'habitude nous appelons les éléments de E les vecteurs et les éléments de K les scalaires. Si sont des vecteurs de E et des scalaires, alors la combinaison linéaire de ces vecteurs ayant comme coefficients ces scalaires est:

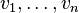
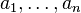
Par convention, une combinaison linéaire ne portant sur aucun vecteur est déclarée nulle.

On peut souhaiter parler de combinaison linéaire sur une infinité de termes ; on convient alors que tous les scalaires intervenant soient nuls sauf un nombre fini : étant une famille quelconque de vecteurs de E et une famille de scalaires presque tous nuls (c'est-à-dire tous nuls sauf éventuellement un nombre fini), la combinaison linéaire de la famille de coefficients est la somme suivante:

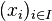
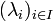
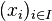
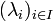
Une relation de dépendance linéaire est une combinaison linéaire égale au vecteur nul. La relation de dépendance linaire triviale est celle donnée par une famille de coefficients tous nuls.

Sous-espace vectoriel engendré

Considérons un corps commutatif K et un espace vectoriel E arbitraires, et soit des vecteurs de E. Il est intéressant de considérer l'ensemble de toutes les combinaisons linéaires de ces vecteurs. Cet ensemble s'appelle le « sous-espace vectoriel engendré » (ou juste « sous-espace engendré ») par ces vecteurs, disons par l'ensemble . Notons ou < A > l'ensemble

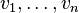
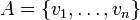
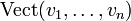
Exemples et contre-exemples

Soit K le corps des nombres réels, et soit E l'espace vectoriel euclidien .

Considérons les vecteurs e₁ = (1,0,0), e₂ = (0,1,0) et e₃ = (0,0,1).

Alors tout vecteur de est une combinaison linéaire de e₁, e₂ et e₃.

Pour le démontrer, considérons un vecteur arbitraire (a₁,a₂,a₃) de , et écrivons:

Généralisations

Si E est un espace vectoriel topologique, alors il est possible de donner un sens à une combinaison linéaire infinie, en utilisant la topologie de E. Par exemple, nous pourrions parler de la somme infinie .

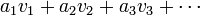
De telles combinaisons linéaires infinies n'ont pas toujours un sens; nous les qualifions de convergentes lorsqu'elles en ont un. Le fait de pouvoir considérer davantage de combinaisons linéaires dans ce cas peut également mener à des concepts plus larges de sous-espace vectoriel engendré, d'indépendance linéaire, et de bases.

Si K est un anneau commutatif au lieu d'être un corps, alors tout ce qui a été dit au-dessus sur les combinaisons linéaires se généralise sans aucun changement. La seule différence est que nous appelons ces espaces E des modules au lieu d'espaces vectoriels.

Si K est un anneau non commutatif, alors la notion de combinaison linéaire se généralise encore, cependant avec une restriction: Puisque les modules sur les anneaux non commutatifs peuvent être des modules à droite ou à gauche, nos combinaisons linéaires peuvent également être écrites à droite ou à gauche, c'est-à-dire avec des scalaires placés à droite ou à gauche, selon la nature du module. C'est simplement une question de multiplication par un scalaire du bon côté.

Une adaptation plus compliquée survient lorsque E est un bimodule sur deux deux anneaux, K_G et K_D.

Dans ce cas, la combinaison linéaire la plus générale ressemble à:

où appartiennent à K_G, appartiennent à K_D, et appartiennent à E.