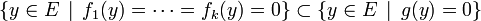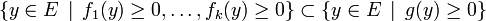Lemme de Farkas - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le lemme de Farkas est un résultat de géométrie convexe essentiel en programmation linéaire où il fonde la théorie de la dualité pour les programmes linéaires, ainsi qu'en théorie des jeux. Il intervient dans la preuve du théorème de Karush-Kuhn-Tucker en programmation non linéaire.
Il affirme, avec quelques précautions techniques nécessaires, qu'étant donnée une famille d'inéquations linéaires (ou affines) dans un espace vectoriel réel de dimension finie, il n'y a pas d'autres conséquences à en déduire que celles qui se déduisent de façon évidente.
On peut donner plusieurs versions du lemme de Farkas, toutes essentiellement équivalentes les unes aux autres.
Ce lemme est un des « théorèmes de l'alternative », qui fournissent pour un système d'inéquations linéaires une condition nécessaire et suffisante d'existence de solution, qui peut s'exprimer comme inexistence de solutions pour un autre problème de forme voisine.
Historique
Ce lemme a été historiquement démontré pour la première fois par Gyula Farkas (en) en 1902 avec une formulation différente. La formulation matricielle est due à Albert William Tucker dans les années 1950.
La version matricielle du lemme
B étant une matrice de réels, on note ici B ≥ 0 lorsque tous les coefficients de B sont positifs ou nuls. La notation tB désigne la matrice transposée de B.
La version matricielle du lemme est la suivante :
Lemme de Farkas, version matricielle — Soient A une matrice de réels de taille (n, k) et b un vecteur-colonne avec n entrées, alors un et un seul des systèmes linéaires suivants a une solution :
- le système Ax = b pour x vecteur-colonne à k entrées vérifiant par ailleurs x ≥ 0 ;
- ou le système tA y ≥ 0 pour y vecteur-colonne à n entrées vérifiant par ailleurs tb y < 0.
La vérification est sans difficulté aucune, une fois qu'on a passé l'obstacle de raccrocher les matrices de cet énoncé aux objets géométriques de l'énoncé précédent.
Pour chaque colonne Cj de A (1 ≤ j ≤ k), notons fj la forme linéaire définie sur Rn par
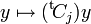
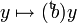
L'existence d'une solution pour la première branche de l'alternative, c'est l'existence d'un k-uplet
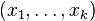
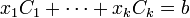
L'existence d'une solution pour la deuxième branche de l'alternative, c'est l'existence d'un y qui soit dans
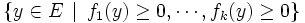
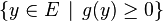
L'équivalence annoncée par le théorème de Farkas garantit donc précisément qu'un et un seul des deux systèmes a une solution.
La version du lemme en géométrie vectorielle
Avant de donner l'énoncé du lemme de Farkas, commençons par rappeler un résultat sur les équations linéaires, suffisamment simple pour ne pas bénéficier d'une dénomination particulière, et dont le lemme de Farkas est la généralisation aux inégalités.
Proposition — Soient f1, ... , fk et g des formes linéaires sur un espace vectoriel E de dimension finie. Alors :
si et seulement si
- g appartient à l'espace vectoriel formé des combinaisons linéaires de f1, ... , fk.
Dit autrement : étant donné un sous-espace vectoriel de E décrit par une liste d'équations cartésiennes, toute autre équation valable sur ce sous-espace s'obtient en combinant de façon immédiate les équations initialement fournies.
Le lemme de Farkas est le résultat analogue pour des systèmes d'inéquations :
Lemme de Farkas, version vectorielle — Soient f1, ... , fk et g des formes linéaires sur un espace vectoriel réel E de dimension finie. Alors :
si et seulement si
- g est une combinaison linéaire à coefficients positifs ou nuls de f1, ... , fk.
Une des preuves passe par l'étape suivante cruciale, qui est aussi parfois appelée lemme de Farkas :
Lemme de Farkas, version topologique — Soient s1, ... , sk des éléments d'un espace vectoriel réel E de dimension finie. L'ensemble des combinaisons linéaires à coefficients positifs ou nuls de s1, ... , sk est fermé dans E.