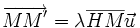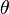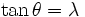Transvection - Définition

Introduction

Dessin d'origine

résultat de la transvection

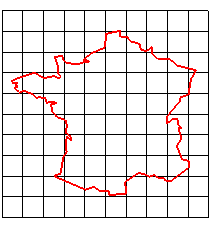
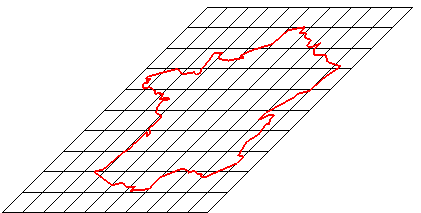
Cet article est à lire en parallèle avec celui sur les dilatations.

Transvection vectorielle

Une transvection d'un espace vectoriel est soit l'identité, soit un endomorphisme de tel que l'ensemble des vecteurs invariants est un hyperplan de (base de la transvection) et (direction de la transvection) est inclus dans (c'est-à-dire que pour tout de , appartient à ).

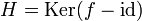
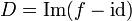
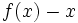
Condition équivalente 1 : est linéaire et .

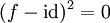
Condition équivalente 2 : il existe une forme linéaire sur et un vecteur invariant tels que pour tout de  :

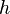
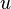
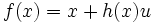
Les transvections sont bijectives ( ) et, en dimension finie, sont de déterminant 1 ; elles engendrent le groupe spécial linéaire de  : . L'ensemble des transvections de base en forme un sous-groupe, isomorphe au groupe additif (à de , faire correspondre la transvection ).

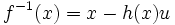
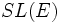
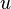
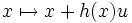
Transvection affine

Une transvection d'un espace affine est soit l'identité, soit une application affine de dans dont l'ensemble des points invariants est un hyperplan de (base de la transvection) et telle que pour tout point le vecteur reste parallèle à . Les vecteurs forment alors une droite vectorielle (direction de la transvection).

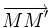
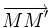
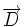
Une transvection affine a pour partie linéaire une transvection vectorielle. Réciproquement, les applications affines ayant pour partie linéaire une transvection vectorielle sont les transvections glissées, composée d'une transvection et d'une translation de vecteur parallèle à la base.

Étant donné deux points et tels que la droite est parallèle à un hyperplan , mais non incluse dans cet hyperplan, il existe une unique transvection de base envoyant sur  ; on obtient facilement l'image d'un point par la construction :

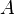
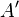
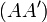
Matrice de transvection

Dans une base de contenant une base de dont l'un des vecteurs est un vecteur directeur de , la transvection a pour matrice une matrice du type avec i < > j. Ces matrices sont appelées matrices de transvection E_{(i < > j)} nul par tout sauf 1 en (i, j) ; elles engendrent le groupe spécial linéaire .

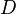
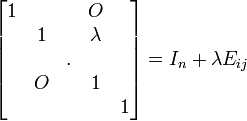
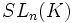
La forme la plus réduite, qui est sa forme de Jordan, de la matrice d'une transvection différente de l'identité est

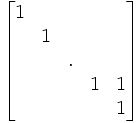
Transvection euclidienne

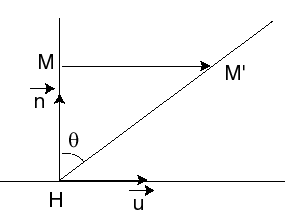Soit une transvection d'un espace euclidien, un vecteur normal et normé de sa base et sa direction de vecteur directeur normé . Avec les notations ci-contre, on a . Le nombre est alors le coefficient de la transvection, et l'angle , défini par , son angle.

Transvection projective

Si l'on plonge l'espace affine dans son complété projectif, en lui adjoignant un hyperplan à l'infini , on sait que l'on peut munir le complémentaire de l'hyperplan d'une structure d'espace affine (les droites qui sont sécantes en un point de dans deviennent parallèles dans et celles qui sont parallèles dans deviennent sécantes en un point de ).

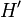
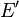
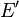
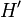
A toute transvection d'hyperplan de est alors associée une application affine de qui n'est autre qu'une translation !

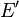
Les transvections sont donc en fait des translations en perspective... Si l'on regarde par avion une translation de vecteur parallèle à la ligne d'horizon, on voit une transvection :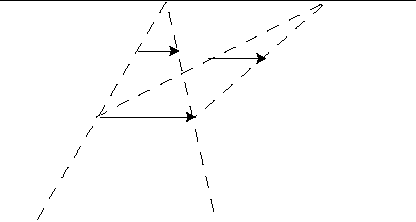

Si maintenant on envoie un autre hyperplan que et à l'infini, la transvection devient une homologie spéciale.

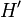
En résumé, il y a, en géométrie projective, identité entre les translations, les transvections, et les homologies spéciales.

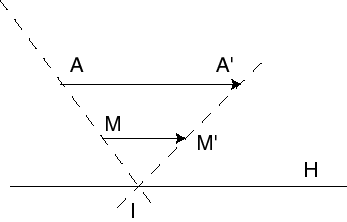
Réalisation d'une transvection par perspective parallèle

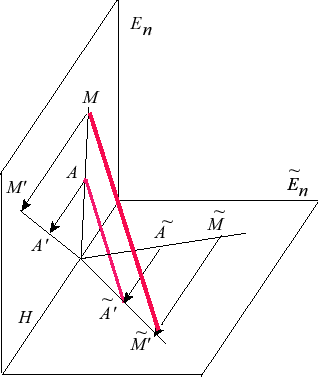
Plongeons l'espace euclidien de dimension n comme hyperplan d'un espace de dimension n+1 et faisons tourner autour de son hyperplan , de façon à en obtenir une copie .

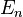
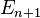
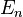
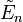
Tout point de a une copie dans , donc aussi l'image de par une transvection de base .

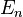
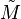
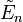
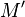
On montre que la droite garde une direction fixe , ce qui montre que s'obtient par projection de dans (projection de base et de direction ).

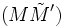
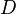
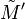
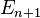
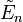
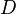
Voir ici une réalisation concrète de ce procédé.