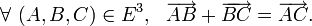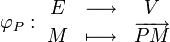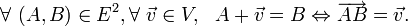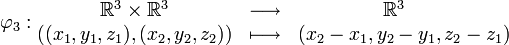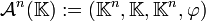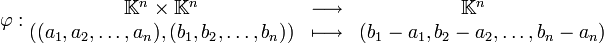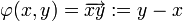Espace affine - Définition

Introduction

Historiquement, la notion d’espace affine est issue du choc dû à la découverte de nouvelles géométries parfaitement cohérentes, mais différant de celle d'Euclide par l'axiome des parallèles. Elles remettaient en cause les notions de longueur et d'angle, qui reposaient elles-mêmes sur celle de distance, et poussèrent à redéfinir l'espace euclidien, en excluant ces notions et tout ce qui s'y rapportait. Le résultat fut une géométrie affine, où l'espace apparait comme une structure algébrique, voisine de celle d'espace vectoriel qui en fut dégagée par la suite (donnant ainsi naissance à l'algèbre linéaire).

Définitions

Il existe de nombreuses manières de définir un espace affine (voir l'article « Structure affine »). Ici, nous supposons donnés :

• un corps ( , + , x ) , noté «   » en abrégé, d'éléments neutres « 0 » pour la loi additive et « 1 » pour la loi multiplicative ;

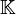
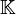
les éléments du corps sont habituellement appelés « scalaires » et notés par des lettres grecques minuscules : ,...

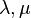
• un espace vectoriel ( , , · ) sur ce corps, noté «   » en abrégé, d'élément neutre «   » ;

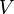
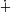
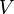
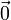
les éléments de l'espace vectoriel sont appelés « vecteurs » et notés par des lettres latines minuscules surmontées d'une flèche : , ,...

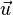
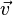
• et un ensemble non vide, à partir duquel nous allons construire notre espace affine ;

ses éléments seront appelés « points » et notés par des lettres latines majuscules : ,...

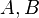
remarque : les couples d'éléments de , éléments de , seront appelés « bipoints », conformément à la tradition. De même, le premier élément d'un tel couple sera appelé « origine » du bipoint, et le second élément « extrémité » du bipoint.

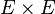
L'espace affine sur le corps , associé à l'espace vectoriel est alors défini comme le quadruplet , où est une loi scalaire binaire, c'est-à-dire une application de dans qui satisfait aux deux propriétés suivantes, appelées axiomes des espaces affines :

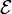
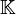
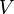
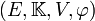
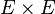
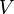
(A1) Pour tout couple de bipoints tels que l'origine du second coïncide avec l'extrémité du premier, la somme des images par est égale à l'image, toujours par , du bipoint formé par l'origine du premier et l'extrémité du second. En d'autres termes :

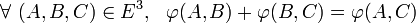
(A2) Pour tout point et tout vecteur, il existe un unique bipoint dont l'origine est le point considéré et dont l'image par est le vecteur considéré. En d'autres termes :

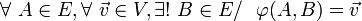
Lorsque le contexte n'est pas ambigu, la notation peut être abrégée, par exemple par E ou par ,...

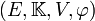
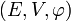
Si l'on note «  » le vecteur , la propriété (A1) s'écrit :

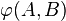
Cette propriété est souvent appelée Relation de Chasles.

La propriété (A2) dit tout simplement que lorsqu'on fixe un point dans , l'application :

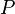
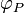
est une bijection. Elle permet aussi de définir une opération (qui est plus utilisée comme une notation) correspondant à l'addition d'un vecteur à un point :

La dimension d'un espace affine est la dimension de l'espace vectoriel qui lui est associé.

L'espace vectoriel est appelé direction de

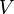
Propriétés élémentaires

Les propriétés suivantes découlent directement de la définition d'espace affine (c'est-à-dire des axiomes (A1) et (A2)). Soient et des points quelconques dans un espace affine . Nous avons alors :

•  ;
•  ;
• (relation de Chasles généralisée)
• (relation du parallélogramme).

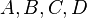
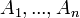
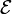
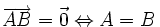
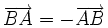
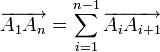
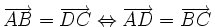
Exemples d'espaces affines

Plan affine

Regardons le plan comme un ensemble de points (sans structure particulière) mais aussi comme un -espace vectoriel.

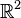
Le quadruplet où est définie par :

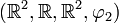
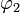
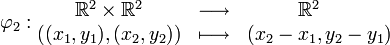
est un -espace affine de dimension 2 (c'est le plan affine).

Espace affine tridimensionnel

Le quadruplet avec :

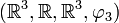
est un espace affine sur de dimension 3.

Espace affine de dimension n

De façon plus générale, si est un corps quelconque, l'espace affine canonique sur de dimension n est le quadruplet :

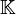
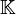
où est vu à la fois comme un espace de points et un -espace vectoriel, et l'application est définie par :

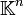
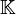
Généralisation : espace affine construit à partir d'un espace vectoriel

De façon encore plus générale, si V est un espace vectoriel sur un corps , on définit l'espace affine canonique associé à l'espace vectoriel V par le quadruplet :

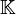
où V est vu à la fois comme un espace de points et un -espace vectoriel, et l'application est définie par :