Nouvelle conjecture de Mersenne - Définition

En mathématiques, la nouvelle conjecture de Mersenne (ou conjecture de Bateman, Selfridge et Wagstaff) est un résultat concernant certains nombres premiers ; il énonce que pour tout nombre naturel impair p, si deux des conditions suivantes tiennent, alors la troisième aussi :

1. ou pour un certain k.
2. est premier (un nombre premier de Mersenne).
3. est premier (un nombre premier de Wagstaff).

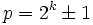
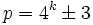
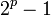
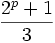
Bibliographie

• P. T. Bateman, J. L. Selfridge and Wagstaff, Jr., Samuel S., The new Mersenne conjecture, Amer. Math. Monthly, 96 (1989) 125-128