Algorithme de Dijkstra - Définition

Introduction

En théorie des graphes, l'algorithme de Dijkstra sert à résoudre le problème du plus court chemin. Il permet, par exemple, de déterminer le plus court chemin pour se rendre d'une ville à une autre connaissant le réseau routier d'une région. Il s'applique à un graphe connexe dont le poids lié aux arêtes est positif ou nul.

L'algorithme porte le nom de son inventeur, l'informaticien néerlandais Edsger Dijkstra et a été publié en 1959.

En théorie de la complexité on démontre que cet algorithme est polynomial.

Principe sur un exemple

Il s'agit de construire progressivement, à partir des données initiales, un sous-graphe dans lequel sont classés les différents sommets par ordre croissant de leur distance minimale au sommet de départ. La distance correspond à la somme des poids des arêtes empruntées.

La première étape consiste à mettre de côté le sommet de départ et à repérer la distance du sommet de départ aux autres sommets du graphe. Cette distance est infinie si aucun arc ne relie le sommet au sommet de départ, elle est de n s'il existe un arc reliant ce sommet au sommet de départ et que le poids le plus faible (s'il existe plusieurs arcs) est de n.

La seconde étape consiste à repérer le sommet qui possède alors la plus courte distance au sommet de départ et à le mettre de côté. Pour tous les sommets restants, on compare alors la distance trouvée précédemment à celle que l'on obtiendrait via le sommet que l'on vient de mettre de côté et on ne conserve que la plus petite des valeurs. et on continue ainsi jusqu'à épuisement des sommets ou jusqu'à sélection du sommet d'arrivée.

Distance entre la ville A et la ville J

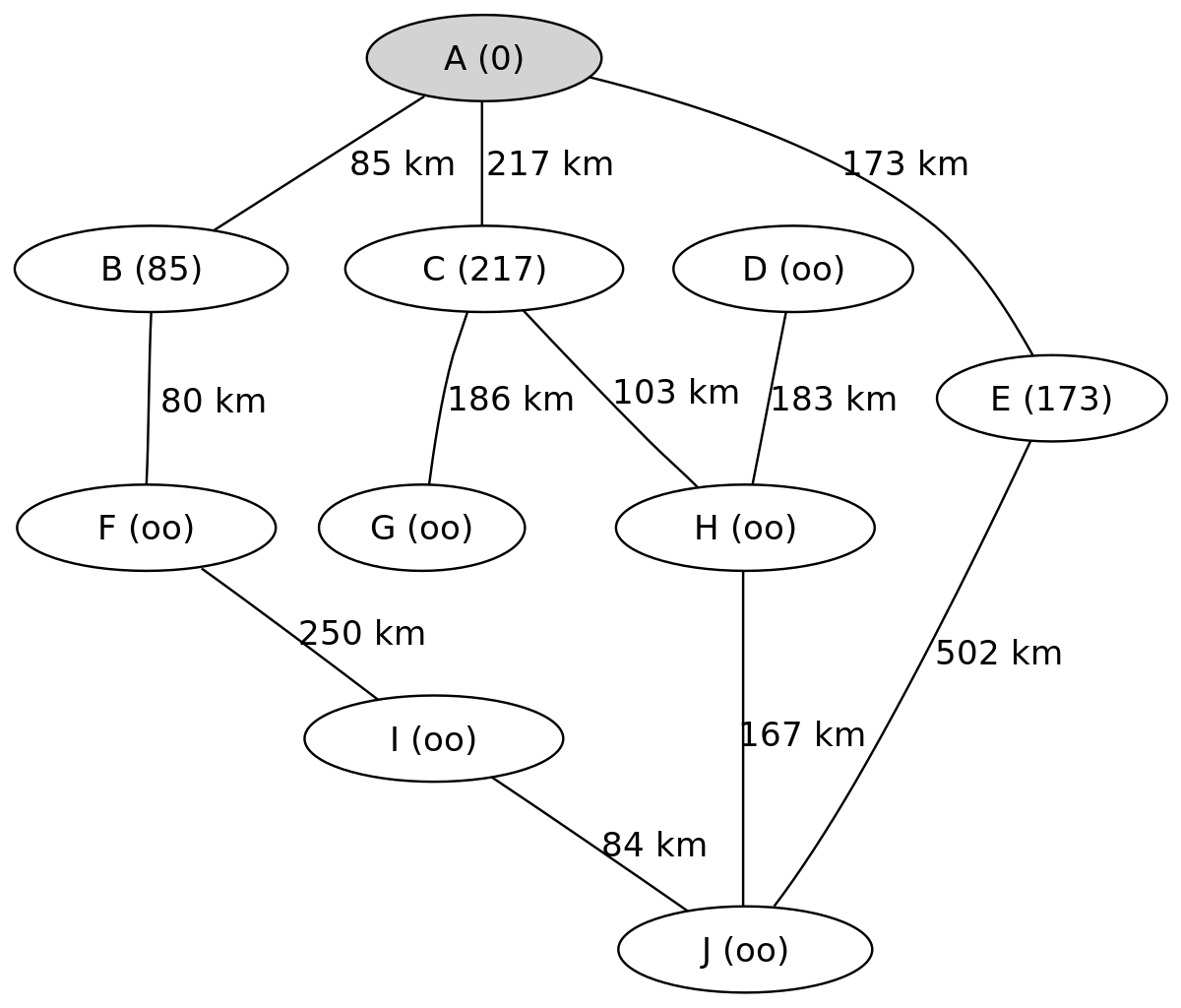
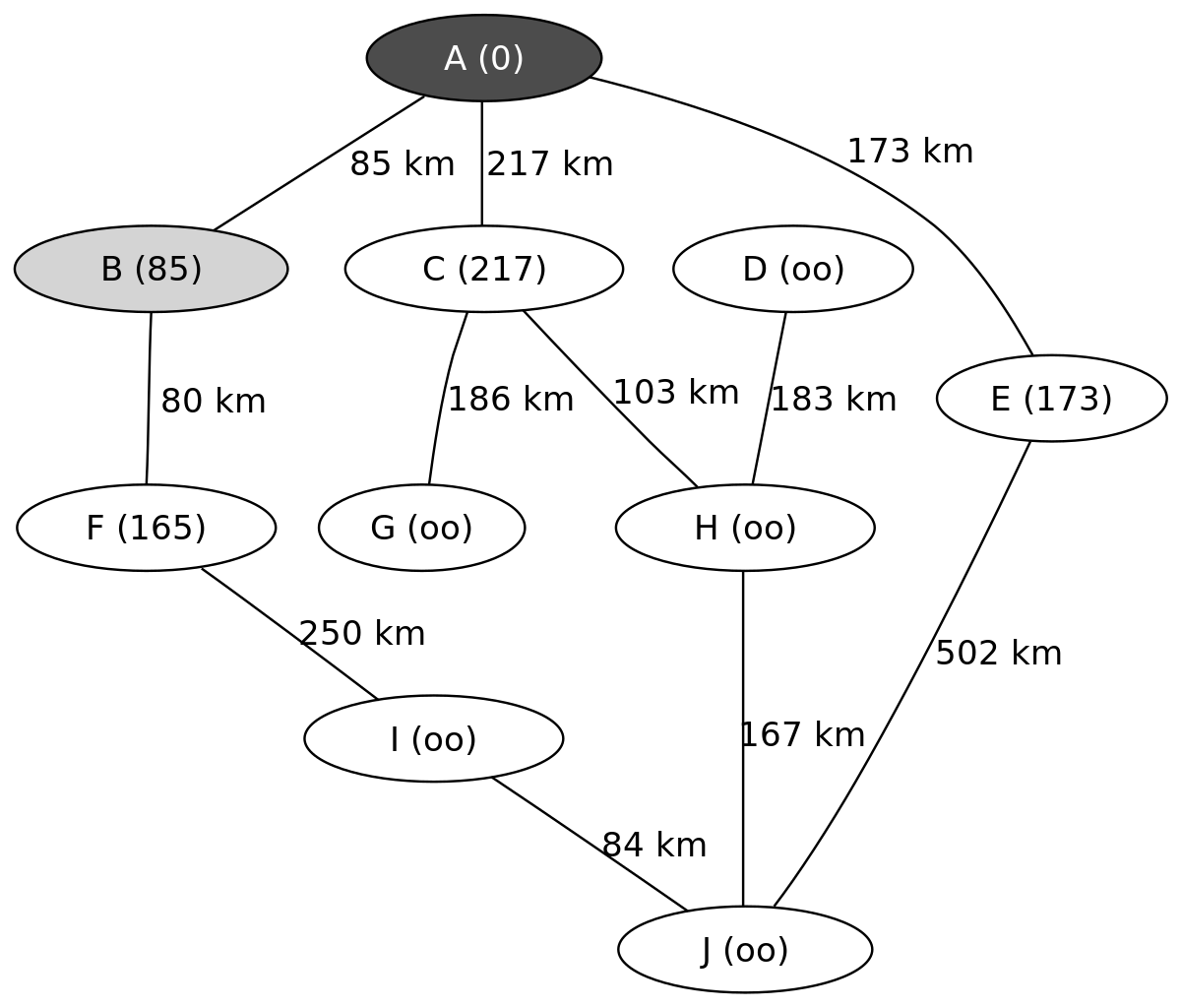
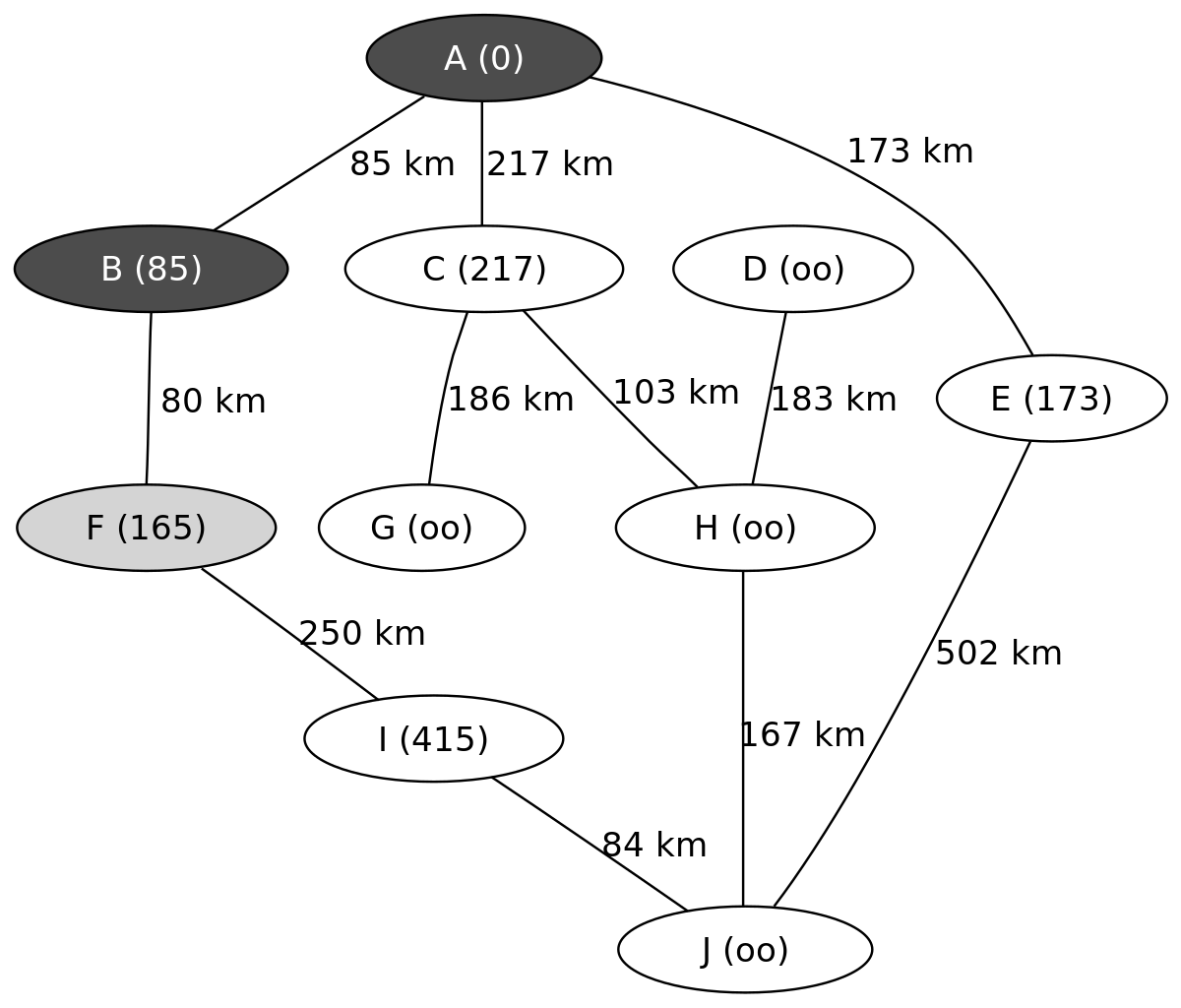
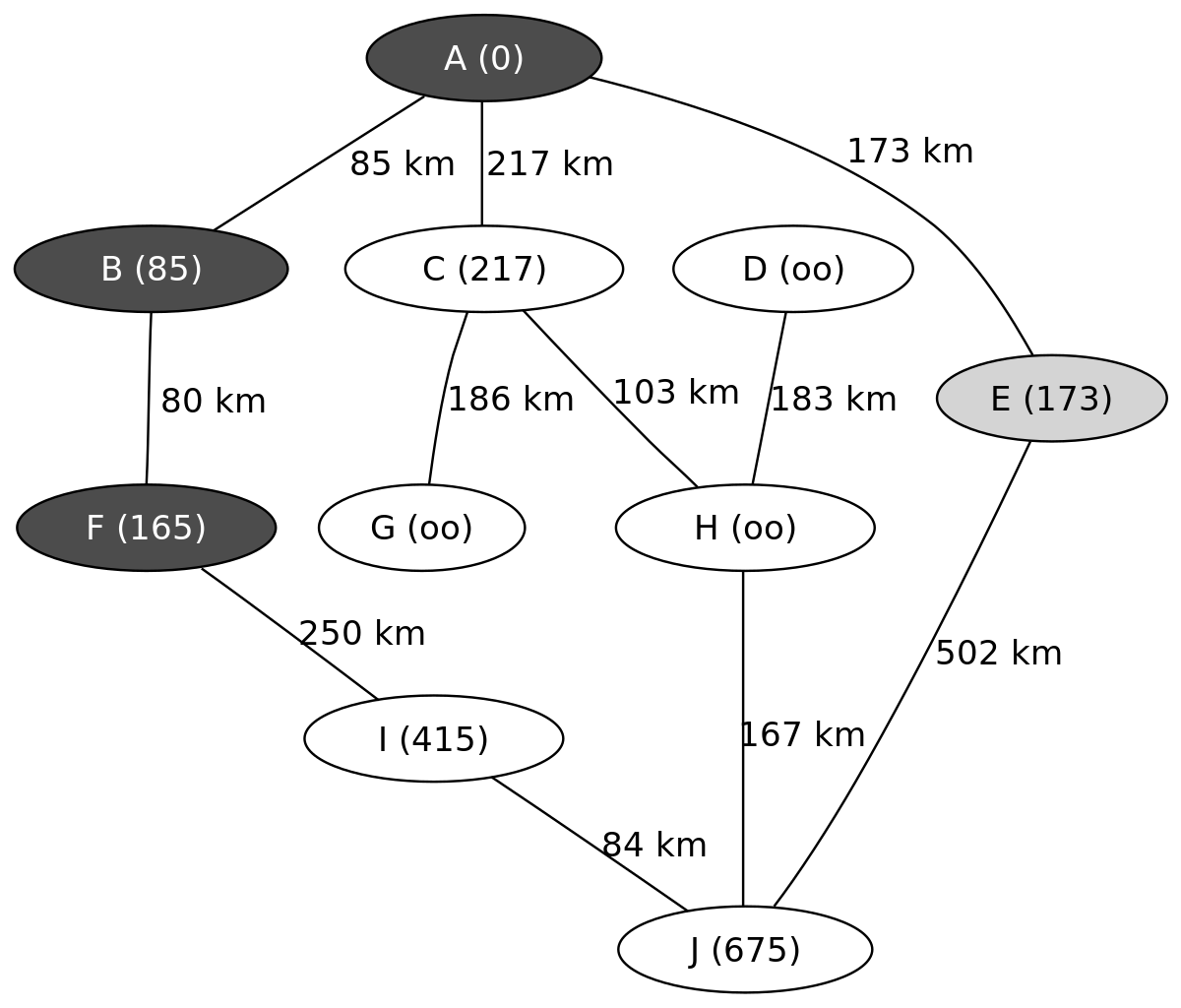
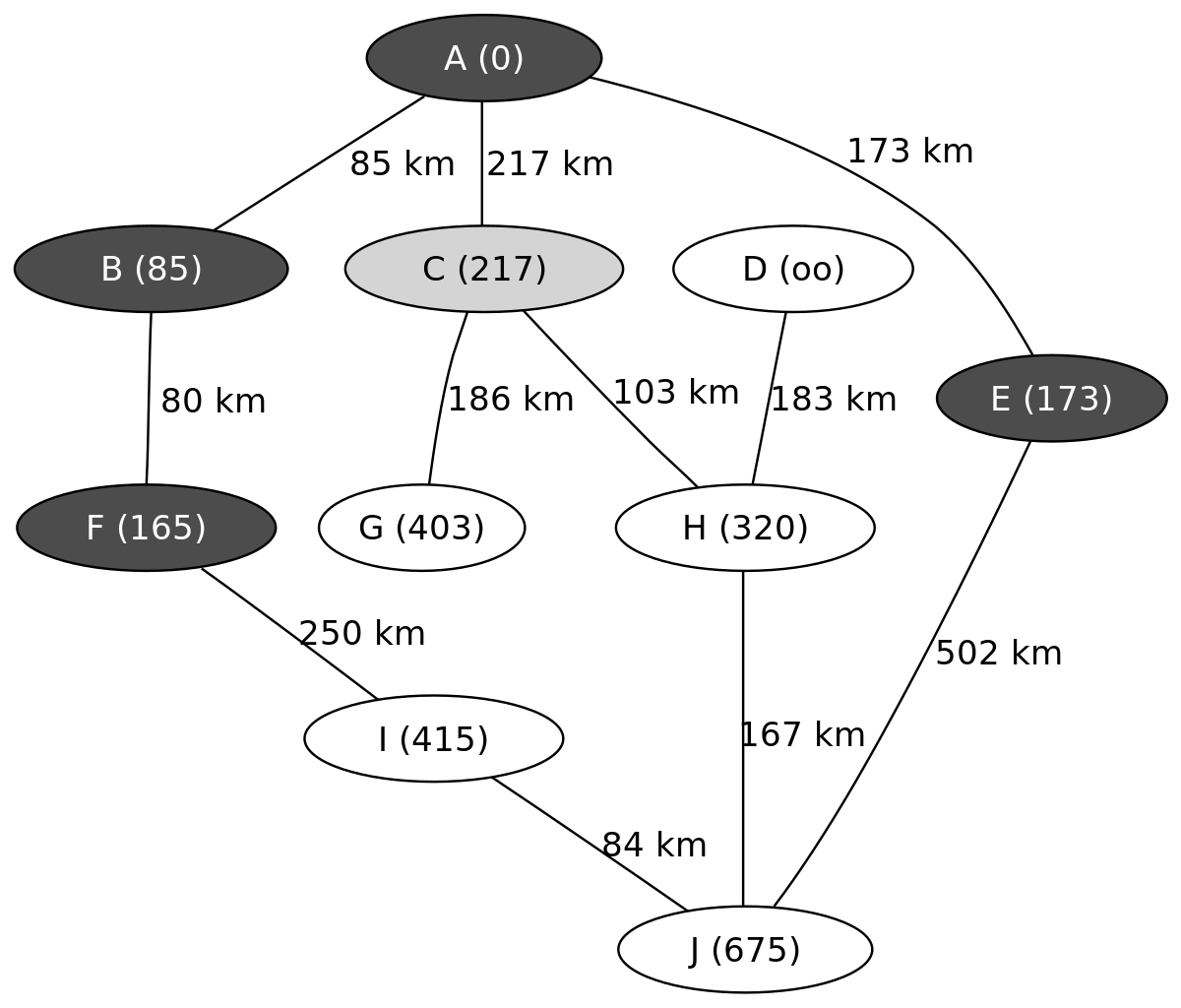
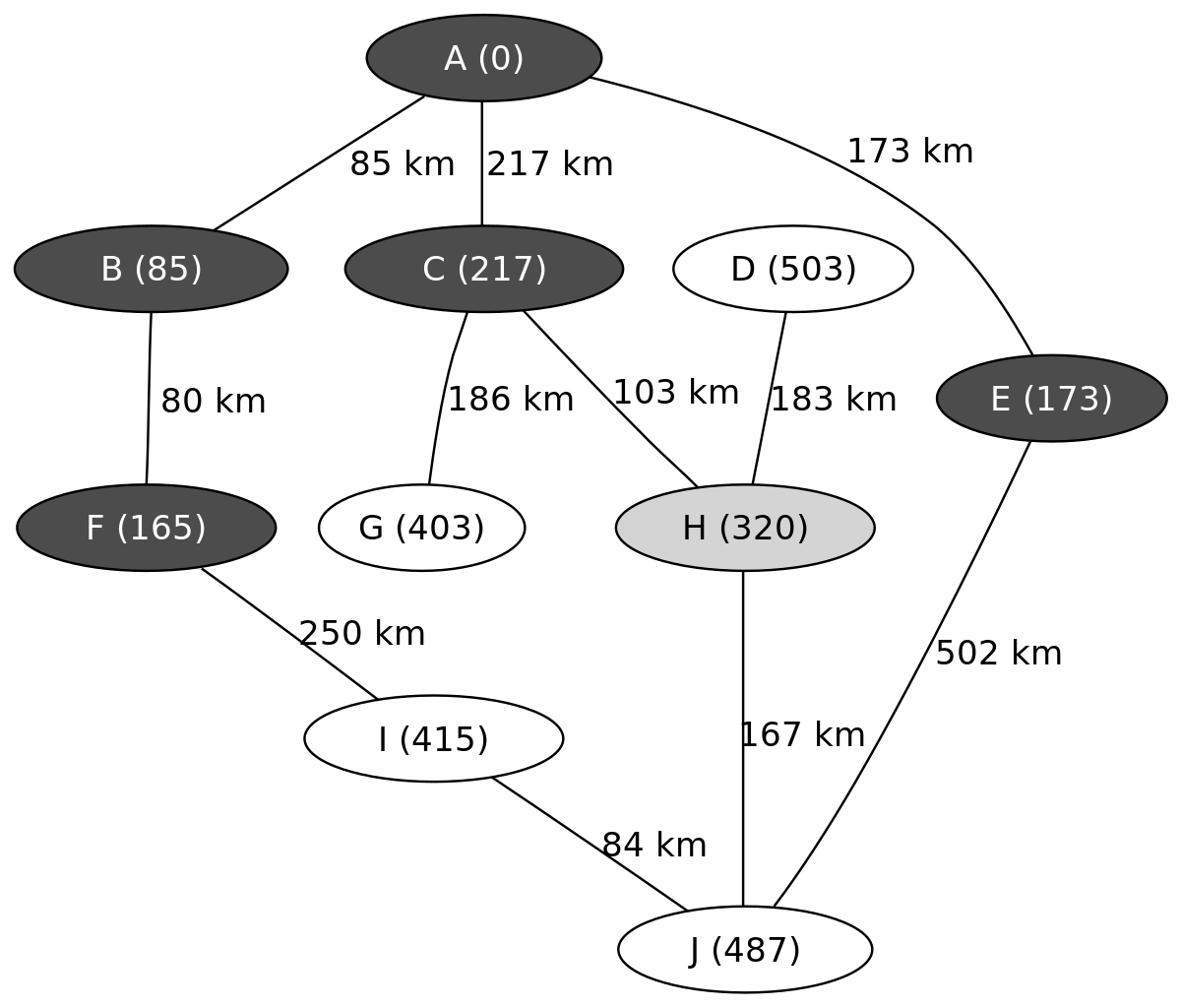
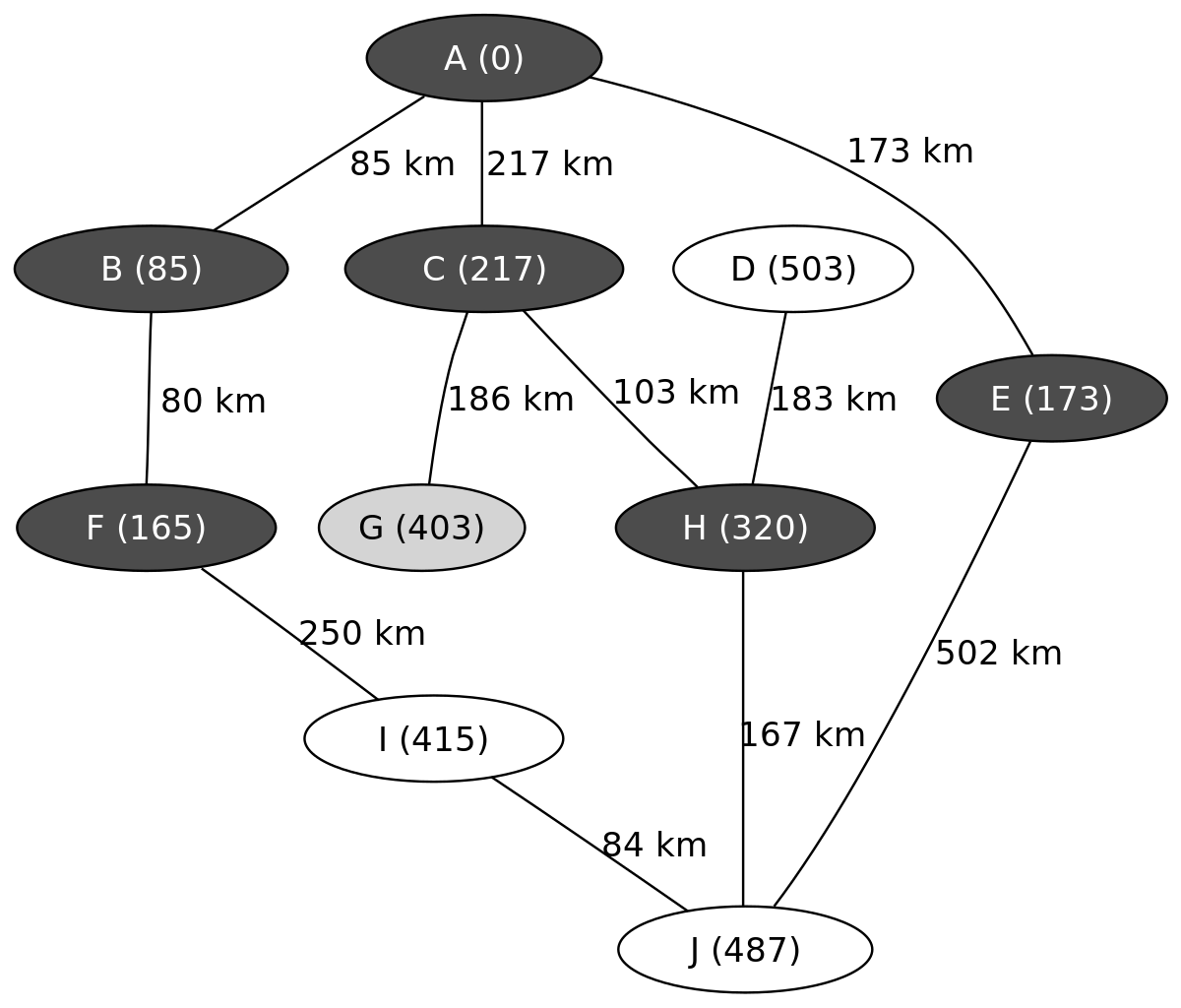
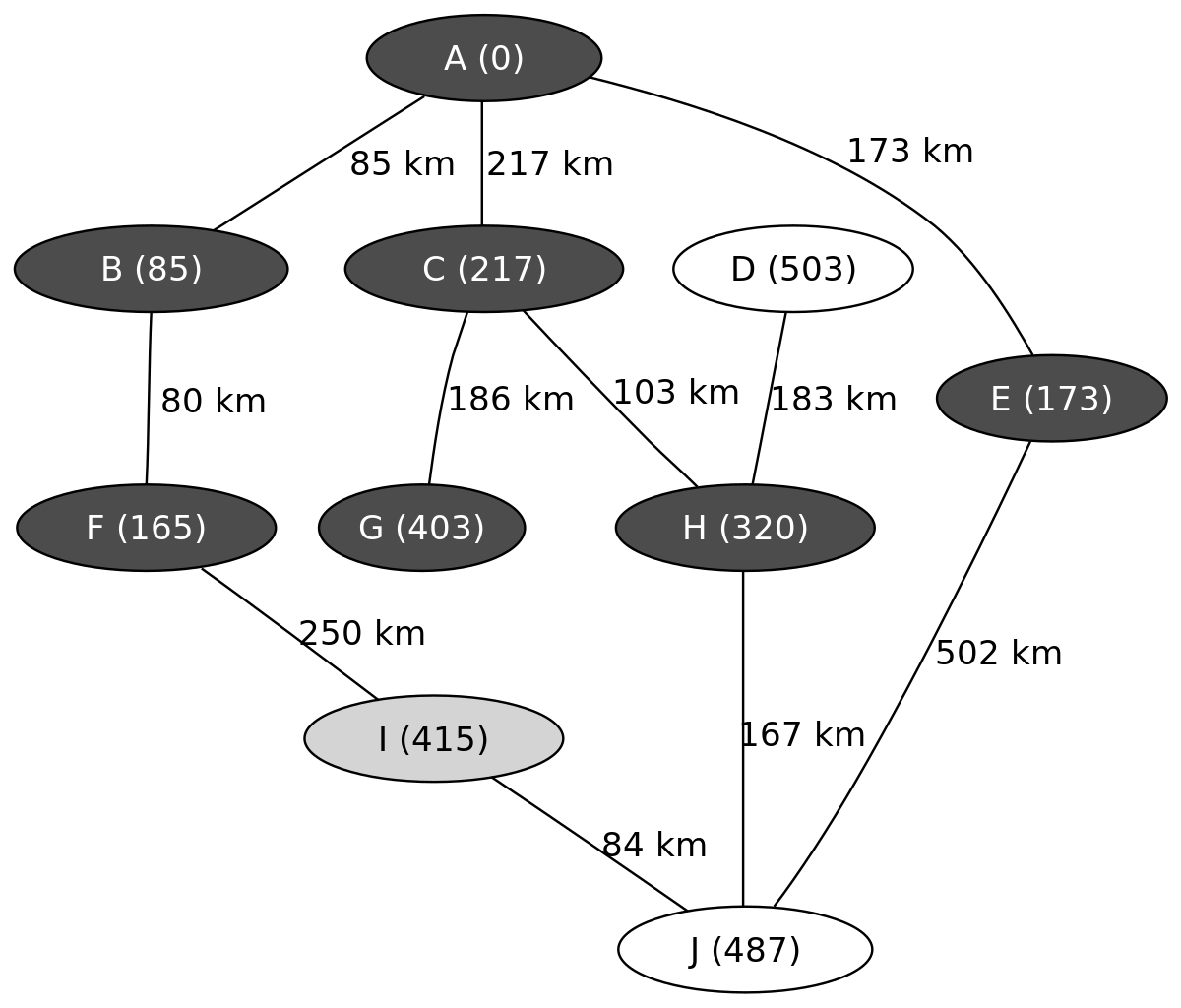
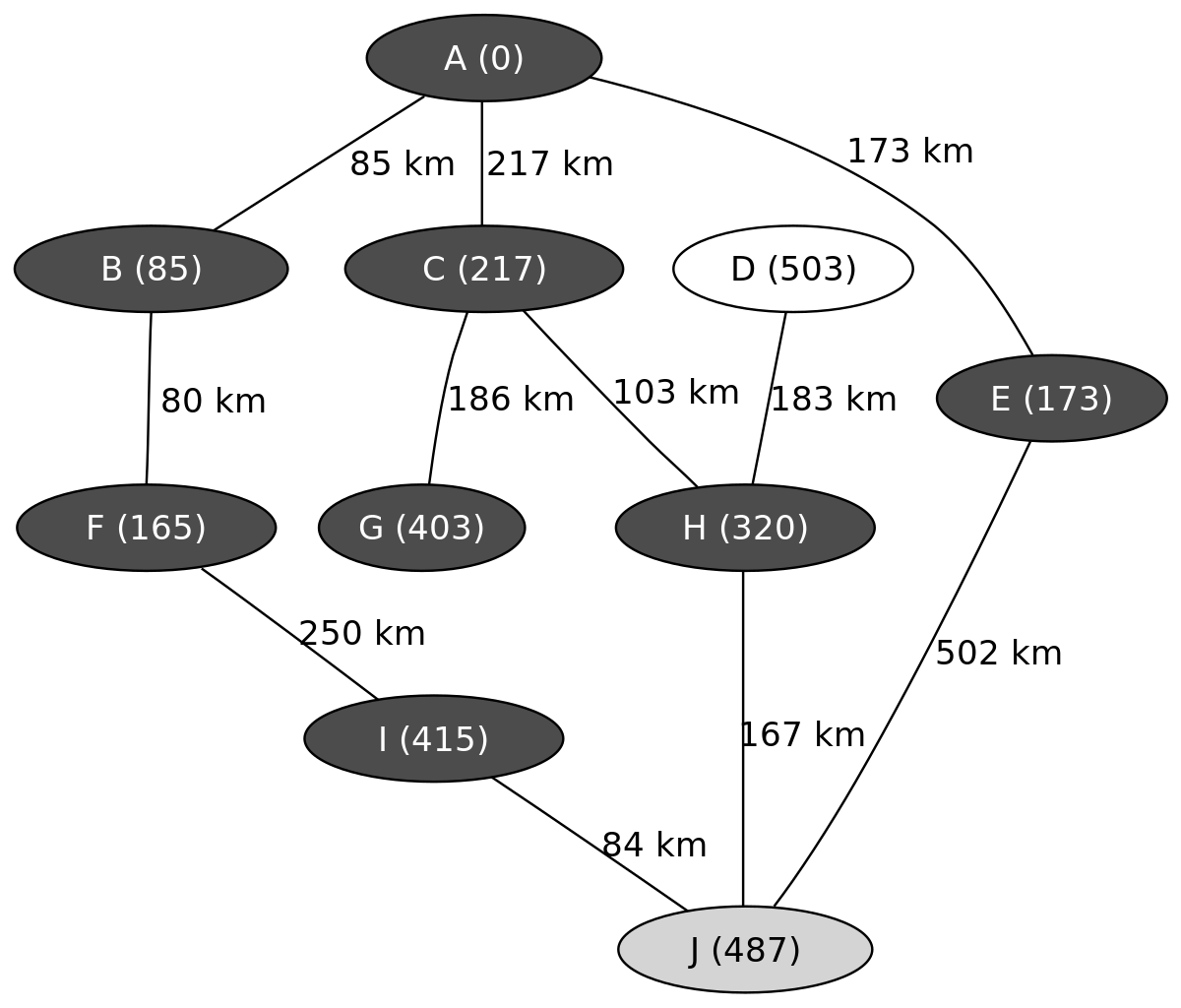
L'exemple suivant montre les étapes successives dans la résolution du chemin le plus court dans un graphe. Les nœuds symbolisent des villes identifiées par une lettre et les arêtes indiquent la distance entre ces villes. On cherche à déterminer le plus court trajet pour aller de la ville A à la ville J.

Étape 1 : à partir de la ville A, 3 villes sont accessibles, B, C, et E qui se voient donc affectées des poids respectifs de 85, 217, 173, tandis que les autres villes sont affectées d'une distance infinie.	Étape 2 : la distance la plus courte est celle menant à la ville B. Le passage par la ville B ouvre la voie à la ville F (85+80 = 165).
Étape 3 : La distance la plus courte suivante est celle menant à la ville F. Le passage par la ville F ouvre une voie vers la ville I (415).	Étape 4 : La distance la plus courte suivante est alors celle menant à la ville E. Le passage par la ville E ouvre une voie vers la ville J (675).
Étape 5 : la distance la plus courte suivante mène alors à la ville C. Le passage par la ville C ouvre une voie vers la ville G (403) et la ville H (320).	Étape 6: la distance la plus courte suivante mène à ville H(320). Le passage par la ville H ouvre une voie vers la ville D et un raccourci vers la ville J (487< 675).
Étape 7 : la distance la plus courte suivante mène à la ville G et ne change aucune autre distance.	Étape 8 : la distance la plus courte suivante mène à la ville I. Le passage par la ville I ouvre un chemin vers la ville J qui n'est pas intéressant (415+ 84 > 487).
Étape 9 : la distance la plus courte suivante mène à la ville J (487).

On connait ainsi le chemin le plus court menant de A à J, il passe par C et H et mesure 487 km.

De nos jours, l'algorithme de Dijkstra est utilisé dans plusieurs applications informatiques telles que les GPS. En outre, Google par exemple a pu introduire cet algorithme pour améliorer plusieurs fonctionnalités sur Google Maps ainsi que Google Earth..

Présentation sous forme de tableau

L'illustration par une série de graphes peut se révéler un peu longue. Il est d'autre part un peu plus difficile de repérer le chemin le plus court à l'issue du dessin. Ainsi l'algorithme de Dijsktra est souvent réalisé à l'aide d'un tableau dans lequel chaque étape correspond à une ligne.

À partir de la matrice des arcs orientés reliant les diverses villes :

On construit un tableau dans lequel les distances d'un sommet au sommet de départ sont regroupées dans une même colonne. Les sommets sélectionnés sont soulignés. Les distances des voies ouvertes par la sélection d'un nouveau sommet sont barrées si elles sont supérieures à des distances déjà calculées. Quand un sommet est sélectionné, c'est que l'on a découvert sa distance minimale au sommet, il est alors inutile de chercher d'autres distances de ce sommet au point de départ.

La construction de ce tableau donne non seulement la distance minimale de la ville A à la ville J mais aussi le chemin à suivre (J - H - C - A) ainsi que toutes les distances minimales de la ville A aux autres villes rangées par ordre croissant.