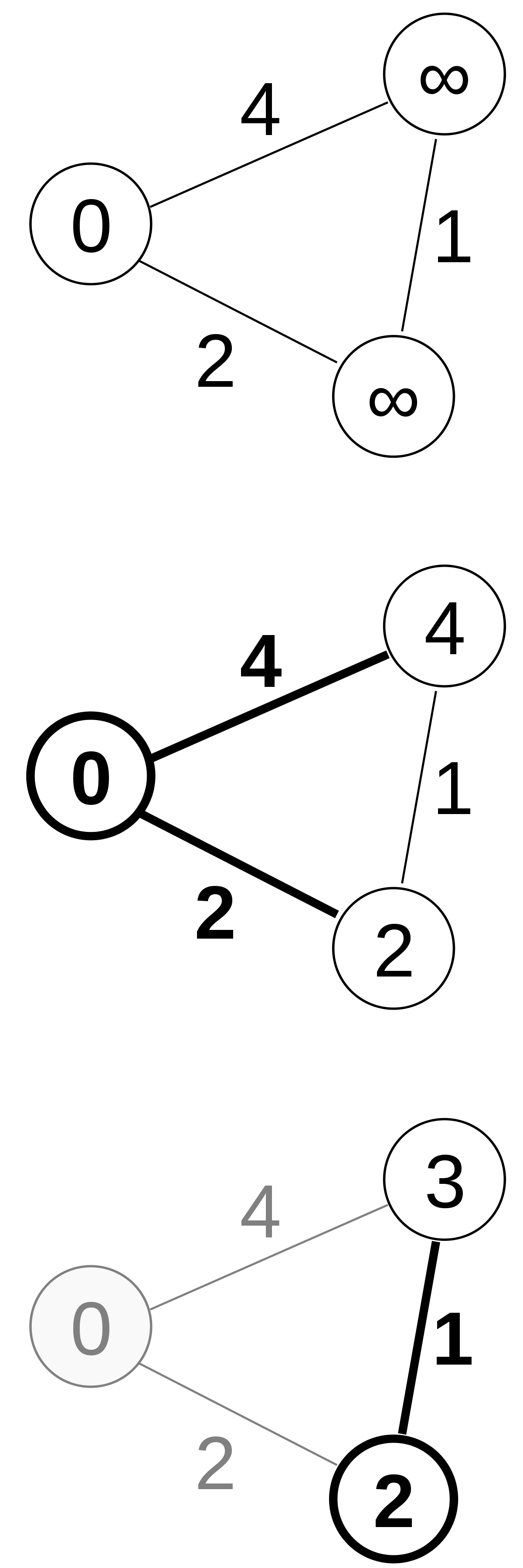
Algorithme de Dijkstra - Définition

Principes

Le poids du chemin entre deux sommets est la somme des poids des arêtes qui le composent. Pour une paire donnée de sommets s_deb (le sommet du départ) s_fin (sommet d'arrivée) appartenant à S, l'algorithme trouve le chemin depuis s_deb vers s_fin de moindre poids (autrement dit le chemin le plus léger ou encore le plus court).

L'algorithme fonctionne en construisant un sous-graphe P de manière à ce que la distance entre un sommet s de P depuis s_deb soit connue et soit un minimum dans G. Initialement P contient simplement le nœud s_deb isolé, et la distance de s_deb à lui-même vaut zéro. Des arcs sont ajoutés à P à chaque étape :

1. en identifiant toutes les arêtes a_i = (s_i1,s_i2) dans tel que s_i1 est dans P et s_i2 est dans G ;

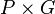
2. en choisissant l'arête a_j = (s_j1,s_j2) dans qui donne la distance minimum depuis s_deb à s_j2 en passant tous les chemins créés menant à ce nœud.

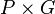
L'algorithme se termine soit quand P devient un arbre couvrant de G, soit quand tous les nœuds d'intérêt sont dans P.

Notations

Le graphe est noté G = (S,A) où :

• l'ensemble S est l'ensemble des sommets du graphe G ;
• l'ensemble A est l'ensemble des arêtes de G tel que : si (s₁,s₂) est dans A, alors il existe une arête depuis le nœud s₁ vers le nœud s₂ ;
• on définit la procédure Poids(s₁,s₂) définie sur A qui renvoie le poids positif de l'arête reliant s₁ à s₂ (et un poids infini pour les paires de sommets qui ne sont pas connectées par une arête).

Codes

Pseudo-code

       fonction Dijkstra (nœuds, fils, distance, debut, fin)           Pour n parcourant nœuds               n.parcouru = infini   // Peut être implémenté avec -1               n.precedent = 0           Fin pour           debut.parcouru = 0           PasEncoreVu = nœuds           Tant que PasEncoreVu != liste vide               n1 = minimum(PasEncoreVu)   // Le nœud dans PasEncoreVu avec parcouru le plus petit               PasEncoreVu.enlever(n1)               Pour n2 parcourant fils(n1)   // Les nœuds reliés à n1 par un arc                   Si n2.parcouru > n1.parcouru + distance(n1, n2)   // distance correspond au poids de l'arc reliant n1 et n2                       n2.parcouru = n1.parcouru + distance(n1, n2)                       n2.precedent = n1   // Dit que pour aller à n2, il faut passer par n1                   Fin si               Fin pour           Fin tant que           chemin = liste vide           n = fin           Tant que n != debut               chemin.ajouterAvant(n)               n = n.precedent           Fin tant que           chemin.ajouterAvant(debut)           Retourner chemin       Fin fonction Dijkstra      

Implémentation Caml

Voici le code d'implémentation Caml :

      (* on suppose données des files de priorité *)      module H : sig        type 'a t        val empty : 'a t        val is_empty : 'a t -> bool        val add : int * 'a -> 'a t -> 'a t        val extract_min : 'a t -> (int * 'a) * 'a t      end             (* l'adjacence est donnée sous la forme d'une fonction: adj v est la liste des voisins de v,         avec leur distance ; la fonction suivante cherche le plus court chemin de v1 à v2 *)      let dijkstra (adj: 'a -> ('a * int) list) (v1:'a) (v2:'a) =        let visited = Hashtbl.create 97 in        let rec loop h =          if H.is_empty h then raise Not_found;          let (w,(v,p)),h = H.extract_min h in            if v = v2 then               List.rev p, w            else              let h =        	  if not (Hashtbl.mem visited v) then begin        	    Hashtbl.add visited v ();        	    List.fold_left (fun h (e,d) -> H.add (w+d, (e, e::p)) h) h (adj v)        	  end else        	    h              in                loop h        in          loop (H.add (0,(v1,[])) H.empty)