Algorithme récursif - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les algorithmes récursifs et les fonctions récursives sont fondamentaux en informatique. Un algorithme est dit récursif s'il s'appelle lui-même.
Les premiers langages de programmation qui ont introduit la récursivité sont LISP et Algol 60 et maintenant tous les langages de programmation modernes proposent une implémentation de la récursivité.
On oppose généralement les algorithmes récursifs aux algorithmes dits impératifs ou itératifs qui s'exécutent sans invoquer ou appeler explicitement l'algorithme lui-même.
Un exemple préliminaire
Commençons par un exemple tiré du Bourgeois gentilhomme (Acte II Scène IV) de Molière. Le héros, Monsieur Jourdain, veut connaître toutes les manières « galantes » d'écrire un billet. De la phrase Belle Marquise, vos beaux yeux, me font mourir d'amour, il pourrait tirer Vos beaux yeux, belle Marquise, d'amour me font mourir, puis Vos beaux yeux, me font mourir, belle Marquise, d'amour, puis Vos beaux yeux, me font mourir d'amour, belle Marquise et ainsi de suite.
Comment Monsieur Jourdain devrait-il procéder pour engendrer toutes ces permutations ? Le mieux pour lui pour être sûr d'y arriver est d'utiliser un procédé récursif. L'un de ceux-ci est le suivant, mais le lecteur peut en imaginer d'autres. Tout d'abord on construit toutes les permutations de la phrase vos beaux yeux -- me font mourir -- d'amour; puis, dans ces permutations, on insère en première position, puis en deuxième position, puis en troisième position, puis en quatrième position le morceau de phrase belle Marquise. L'algorithme est récursif parce qu'il s'invoque lui-même. En effet, pour construire toutes les permutations de belle Marquise -- vos beaux yeux -- me font mourir -- d'amour, il faut construire toutes les permutations de vos beaux yeux -- me font mourir -- d'amour. De plus, l'algorithme est bien un algorithme général, car si Monsieur Jourdain veut améliorer son côté poétique et veut construire, comme le lui dit son maître de philosophie, toutes les permutations de la phrase belle Marquise -- vos beaux yeux -- me font -- mourir -- d'amour, qui a maintenant cinq constituants il procédera de la même façon et encore de la même façon pour la phrase belle Marquise -- vos beaux yeux -- me font -- mourir -- d'amour -- pour vous, qui a six constituants.
Un autre exemple : le nombre de décompositions d'un entier naturel en au plus q sommants
Nous allons considérer un cas tiré des mathématiques où l'approche récursive s'impose (voir l'article Fonction partage d'un entier).
- Un exemple:
Un sommant est un naturel positif qui entre dans une somme quand on décompose un nombre en somme de naturels. Ainsi, les décompositions de 5 en au plus 3 sommants sont 5, 4+1, 3+2, 3+1+1, 2+2+1, si on écrit d(5,3) le nombre de décomposition de 5 en au plus 3 sommants, on a d(5,3) = 5 et si on écrit d'(5,3) le nombre de décomposition de 5 en exactement 3 sommants, on a d'(5,3) = 2, car ces décompositions sont 3+1+1 et 2+2+1.
- Les cas dégénérés:
Si p = 0 alors 0 n'a qu'une décomposition en au plus q sommants, à savoir celle constituée d'aucun sommant. On a donc d(0,q) = 1. Il n'y pas de décomposition de p strictement positif en au plus zéro sommants, donc d(p + 1,0) = 0. Si p < q, il n'y a pas de décomposition de p en exactement q sommants, donc le nombre de décompositions de p en au plus q sommants est le nombre de décompositions de p en au plus p sommants, ce qui s'écrit: si p < q alors d(p,q) = d(p,p).
- Le cas général:
On voit facilement que le nombre de décompositions de p en au plus q sommants est le nombre de décompositions de p en exactement q sommants plus le nombre de décompositions de p en au plus q-1 sommants. Donc
-
- d(p,q) = d'(p,q) + d(p,q − 1).
Or si p a exactement q sommants cela veut dire que tous ces sommants sont strictement positifs, on peut donc leur retirer 1. Or si on retire 1 à chacun de ces sommants on obtient une décomposition de p - q en au plus q sommants, d'où:
-
- d'(p,q) = d(p − q,q)
et finalement
-
- d(p,q) = d(p − q,q) + d(p,q − 1).
Autrement dit, si
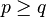
On a bien un énoncé récursif.
- Retour à l'exemple:
on a donc (le lecteur est invité à faire tous les calculs intermédiaires)
-
- d(5,3) = d(2,3) + d(5,2) = d(2,2) + d(3,2) + d(5,1) = d(0,2) + d(2,1) + d(1,2) + d(3,1) + d(4,1) + d(5,0) = ... = 1 + 1 + 1 + 1 + 1 + 0 = 5..
Voici la forme complète de la fonction récursive:
d(p, q) = si p = 0 alors 1 sinon si q = 0 alors 0 sinon si q > p alors d(p, p) sinon d(p-q, q) + d(p, q-1)

















































