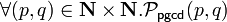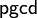Algorithme récursif - Définition

Un exemple plus mathématique : la factorielle

Prenons maintenant un exemple issu des mathématiques, celui de la factorielle. Celle-ci se définit intuitivement pour des entiers positifs par la fonction suivante :

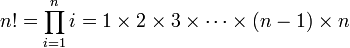
L'idée de la récursivité est d'utiliser une définition équivalente, à savoir une suite récurrente:

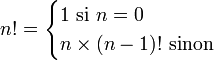
Le lecteur intéressé pourra regarder en le codage de la factorielle dans différents langages de programmation.

Préciser que factorielle(0) = 1 est fondamental : sans cela la fonction ne serait pas définie et l'algorithme s'invoquerait indéfiniment. Le cas n = 0 est appelé cas de base. Sans sa présence, l'algorithme ne peut pas se terminer. L'autre cas est appelé cas de propagation c'est lui qui contient l'appel récursif. On peut programmer ainsi d'autres suites telles que la suite de Fibonacci, tandis que la fonction suivante :

      let rec syracuse n =         if (n = 0) or (n = 1) then 1         else if (n mod 2 = 0) then syracuse(n/2)         else syracuse(3*n + 1)       ;;      

définit la fonction identiquement égale à 1 si la conjecture de Syracuse est vraie.

Mais, comme nous l'avons vu dans l'exemple préliminaire, les algorithmes récursifs ne se limitent évidemment pas au calcul de suites récurrentes et de fonctions sur les entiers naturels. Ils permettent de travailler sur des structures de données définies récursivement comme les chaînes de caractères, les listes ou les arbres, ou plus généralement sur des ensembles munis d'une relation bien fondée. Se distinguent ainsi récursivité structurelle et récursivité numérique (ou récursivité sur les entiers). Le tri, le problème des tours de Hanoï et la génération des permutations (c'est-à-dire la généralisation de l'exemple de Monsieur Jourdain) sont également des exemples célèbres d'application d'algorithmes récursifs.

Prouver la correction d'un algorithme récursif

Puisqu'un algorithme (récursif ou non) est supposé résoudre un problème précis, il faut s'assurer qu'il fait bien la tâche qu'on lui assigne. Cela peut se faire rigoureusement et c'est pour cela que l'on parle de preuve. En fait, il faut vérifier deux propriétés: premièrement l'algorithme se termine et deuxièmement si l'algorithme se termine, il fait bien ce qu'on attend de lui (correction partielle). Dans le cas des algorithmes récursifs, ces méthodes sont spécifiques.

Le problème de la terminaison

Il s'agit de fournir un ordre sur les paramètres de l'algorithme. Cet ordre doit d'abord ne pas avoir de chaînes infinies descendantes (on dit qu'il doit être bien fondé) et ensuite il doit être tel que si on invoque l'algorithme avec des paramètres, les invocations suivantes plus internes doivent se faire avec des paramètres plus petits pour l'ordre.

Le théorème de terminaison

Soient un algorithme récursif défini sur un ensemble et une relation d'ordre bien fondée sur .

étant donné, on note, A_x l'ensemble des tels que appelle .

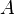
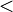
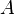
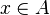
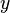
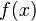
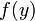
Soit , si, , alors se termine.

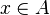
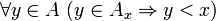
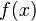
La terminaison de la fonction d qui calcule le nombre de décompositions de p en au plus q sommants

L'ordre que l'on prend est l'ordre de lexicographique sur . On a

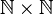
• (p,q) > (p',q') si
  • p > p'
  • ou p = p' et q > q'.

Cet ordre est bien fondé.

La terminaison de la fonction syracuse

La terminaison d'un algorithme récursif peut être un problème extrêmement difficile. Ainsi personne n'a jusqu'à présent été capable de démontrer que la fonction syracuse présentée plus haut se termine pour toute valeur de n. Si c'était le cas, elle définirait effectivement la fonction identiquement égale à 1.

Le problème de la correction partielle

Il faut monter que si les appels internes à l'algorithme font ce qu'on attend d'eux, alors l'algorithme entier fait ce qu'on attend de lui. Dans le cas de Monsieur Jourdain, il faut montrer que si on part d'une suite de toutes les permutations de n-1 éléments, on aboutira à une suite de toutes les permutations de n éléments.

La correction partielle sur l'exemple du pgcd

Prenons l'exemple du , il s'agit de montrer que si et sont positifs alors

• ,

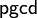
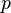
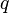
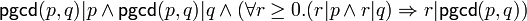
ce qui est la caractérisation du plus grand diviseur commun de deux nombres où signifie que divise (on a, en particulier, pour tout ). Appelons cette propriété.

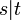
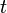
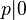
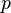
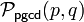
Pour montrer la correction de l'algorithme ci-dessus, on suppose et on essaie de montrer où est la fonction .

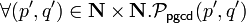
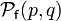
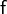
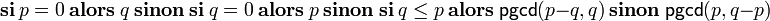
On procède par cas.

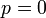
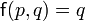
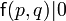
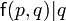
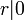
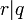
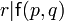
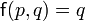
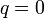
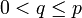
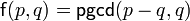
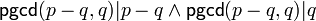
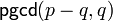
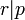
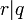
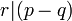
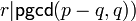
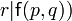
• Si alors et donc , mais aussi . De plus, si et si alors clairement , puisque précisément .
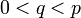
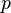
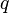
• Si on obtient le même résultat.
• Si , on a , d'autre part si on a alors divise la somme donc . D'autre part, si et alors par hypothèse et donc et donc , c.q.f.d.
• Si , on raisonne comme ci-dessus en inversant les rôle de et .

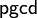
De la démonstration ci-dessus, on déduit que si l'algorithme de se termine alors il satisfait:

et donc calcule bien le plus grand commun diviseur.