Anneau d'ensembles - Définition

Introduction

Un anneau d'ensembles est une classe non vide de parties d'un ensemble X vérifiant deux propriétés de stabilité. Le concept, très voisin de celui d'algèbre d'ensembles, est utilisé en théorie de la mesure pour initialiser les constructions de mesures classiques qu'on étendra ensuite à la tribu engendrée par l'anneau. Vus comme parties de l'anneau de Boole de toutes les parties de X (considéré comme un pseudo-anneau), ils en sont les sous-anneaux (non nécessairement unitaires).

Définition

Une minorité de sources exigent également que X ne soit pas vide ; cette hypothèse supplémentaire n'est nulle part utilisée dans le présent article.

Utilisations en théorie de la mesure

Dans la généralisation de la construction de la mesure de Lebesgue que synthétise le théorème d'extension de Carathéodory, une mesure est construite sur une σ-algèbre par un procédé d'extension relativement sophistiqué, mais dont la première étape est assez simple : on construit d'abord les valeurs de la mesure sur les éléments d'un anneau d'ensembles . La construction peut avoir été initiée sur un semi-anneau d'ensembles qui engendre lui-même (comme anneau d'ensembles).

Dans l'exemple de la mesure de Lebesgue sur la droite réelle, le semi-anneau qui initie la construction peut être l'ensemble des intervalles bornés de , et l'anneau est alors l'ensemble des réunions finies d'intervalles bornés.

Il existe des variantes de cette construction qui font intervenir des variantes de la notion de σ-algèbre : on appelle dans cette optique σ-anneau un anneau stable par réunion dénombrable et δ-anneau un anneau stable par intersection dénombrable.

Propriétés élémentaires

Soit un anneau d'ensembles. Alors :

• l'ensemble vide appartient à (l'écrire pour un élément A de l'ensemble non vide ) ;

• est stable par différence symétrique (on peut en effet écrire ) ;

• est stable par intersection (on peut en effet écrire ) ;

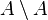
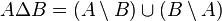
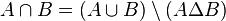
Toute algèbre d'ensembles est un anneau d'ensembles (on peut en effet écrire , où on note ^cE le complémentaire d'une partie E). Il existe en revanche des anneaux d'ensembles qui ne sont pas des algèbres d'ensembles, l'exemple le plus simple étant celui de .

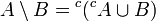
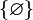
Un anneau d'ensembles sur X est une algèbre d'ensembles si et seulement si X appartient à l'anneau.

Anneaux d'ensembles et algèbres de Boole

On peut donner la définition des anneaux d'ensembles sous une forme alternative :

Les remarques faites plus haut ont montré que la définition initiale entraînait cette caractérisation. Réciproquement, si vérifie les trois hypothèses qui précèdent, il est stable par différence ensembliste (puisque ) et par réunion (puisque ) et est donc un anneau d'ensembles.

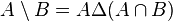
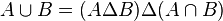
On rappelle que l'algèbre de Boole de toutes les parties de l'ensemble X est munie d'une structure d'anneau de Boole, l'addition étant la différence symétrique (de neutre ) et la multiplication étant l'intersection (de neutre X). Pour cette structure, les anneaux de parties sont donc les sous-groupes additifs stables par la multiplication : ce sont donc les sous-structures pour la structure de pseudo-anneau. Quant aux algèbres de parties, ce sont, pour leur part, les sous-groupes additifs stables pour la multiplication et contenant le neutre de celle-ci : ce sont donc les sous-structures pour la structure d'anneau (unitaire).