Optique - Définition

Introduction

L'optique est la branche de la physique qui traite de la lumière, du rayonnement électromagnétique et de ses relations avec la vision.

Introduction

Historiquement, l'optique, apparue dès l'Antiquité, a d'abord été géométrique.

L'optique géométrique propose une analyse de la propagation de la lumière basée sur des principes simples : la propagation rectiligne et le retour inverse. Elle a pu expliquer les phénomènes de la réflexion et de la réfraction. Elle s'est perfectionnée jusqu'au XVIII^e siècle, où la découverte de nouveaux phénomènes, tels que la déformation de la lumière au voisinage d'obstacles ou le dédoublement de la lumière lors de la traversée de certains cristaux, a conduit au XIX^e siècle au développement de l'optique physique ou ondulatoire.

L'optique ondulatoire considère la lumière comme une onde ; elle prend en compte les phénomènes d'interférence, de diffraction et de polarisation.

Au début du XX^e siècle les théories d'Einstein sur la nature corpusculaire de la lumière donneront naissance au photon et à l'optique quantique. Les physiciens sont alors contraints d'admettre que la lumière présente à la fois les propriétés d'une onde et d'un corpuscule. À partir de là, Louis de Broglie considère, au travers de la mécanique ondulatoire, que si le photon peut se comporter comme un corpuscule, alors, à l'inverse, les corpuscules tels que les électrons ou les protons peuvent se comporter comme des ondes.

Les différentes approches

Optique géométrique

L'optique géométrique s'est développée sur la base d'observations simples et repose sur deux principes et des lois empiriques :

• la propagation rectiligne dans un milieu homogène et isotrope ;
• le principe du retour inverse qui exprime la réciprocité du trajet lumineux entre source et destination ;
• les Lois de Snell-Descartes pour la réflexion et la réfraction.

La résolution des problèmes se fait à l'aide de constructions géométriques (tracés de droites matérialisant les rayons, calculs d'angles), d'où le nom d'optique géométrique. Elle donne de bons résultats tant que l'on ne cherche pas à modéliser des phénomènes liés à la polarisation ou aux interférences et qu'aucune dimension du système n'est comparable ou inférieure à la longueur d'onde de la lumière utilisée.

L'optique géométrique permet de retrouver la quasi-totalité des résultats concernant les miroirs, les dioptres et les lentilles ou leurs combinaisons en doublet et systèmes optiques constituant notamment les instruments d'optique.

De plus, dans le cadre de l'approximation de Gauss, l'optique géométrique donne des relations mathématiques linéaires permettant l'usage d'outils mathématiques tels que les matrices et la systématisation des calculs par ordinateur.

Optique ondulatoire ou optique physique

Alors que l'optique géométrique est une optique purement phénoménologique et ne fait pas d'hypothèse sur la nature de la lumière, hormis éventuellement qu'elle transporte de l'énergie, l'optique ondulatoire (parfois appelée “optique physique”) modélise la lumière par une onde.

Le modèle de l'onde scalaire (principe de Huygens-Fresnel) permet d'interpréter les phénomènes de diffraction (lors du passage par un trou, une fente étroite, près d'un bord...) et d'interférences. Les calculs reposent alors sur la somme des amplitudes d'ondes sinusoïdales qui se superposent, somme qui, suivant le déphasage, peut conduire à un résultat nul. La superposition de deux faisceaux peut ainsi donner l'obscurité. C'est ce qu'on observe au niveau des zones sombres des figures d'interférence ou de diffraction.

Il faut ensuite considérer qu'il s'agit d'une onde transversale, si l'on veut interpréter les phénomènes de polarisation. Enfin, Maxwell permettra de comprendre que les ondes lumineuses ne sont que des ondes électromagnétiques caractérisées par un domaine de longueurs d'ondes qui les rend visibles pour l'homme.

L'optique physique est le nom d'une approximation haute fréquence (petite longueur d'onde) couramment utilisée en optique, en physique appliquée ou en ingénierie électrique. Dans ces contextes, c'est une méthode intermédiaire entre l'optique géométrique, qui ignore les effets ondulatoires, et l'optique ondulatoire qui est une théorie physique exacte.

Cette approximation consiste à utiliser les rayons de l'optique géométrique pour estimer les champs sur une surface puis intégrer ces champs sur toute la surface éclairée pour déterminer les champs transmis et réfléchis.

Dans les domaines optiques et radiofréquences, cette approximation est utilisée pour calculer les effets d'interférences et de polarisation et estimer les effets de diffraction. Comme toutes les approximations hautes fréquences, l'approximation de l'optique physique gagne en pertinence à mesure que l'on travaille avec de hautes fréquences.

La méthode consiste généralement à approcher la densité surfacique de courant électrique à la surface d'un objet par la densité de courant induite par le champ magnétique incident , comme c'est le cas sur un plan métallique infini. C'est pour cela que l'approximation de l'optique physique est parfois appelée “hypothèse du plan tangent”.

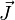
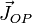
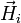
La densité de courant électrique au point Q de la surface éclairée est alors calculée par la relation :

où correspond au vecteur normal unitaire extérieur à la surface éclairée. Dans les zones d'ombre (surfaces non-éclairées selon l'hypothèse de l'optique géométrique), la densité de courant est considérée comme nulle. Les champs rayonnés par la surface sont ensuite calculés en intégrant la densité de courant électrique sur la surface éclairée avec des expressions intégrales des équations de Maxwell, par exemple les équations intégrales de Stratton-Chu, de Kottler ou de Franz.

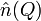
À cause de l'hypothèse effectuée sur la densité de courant électrique à la surface d'un objet, cette approximation est d'autant plus correcte lorsque les objets étudiés sont grands devant la longueur d'onde et avec des surfaces lisses. Pour la même raison, cette densité de courant approchée est inexacte à proximité des discontinuités comme des arêtes ou les frontières entre la zone éclairée et les zones d'ombre. De plus, cette approximation ne rend pas compte des ondes rampantes.

Optique quantique

Les problèmes liés au rayonnement du corps noir et à l'effet photoélectrique ont amené à considérer que la lumière était composée de paquets d'énergie (licht quanta, en allemand, d'après Einstein).

Plus tard, l'effet Compton a conduit à considérer la lumière comme constituée de particules à part entière : les photons.

Ceux-ci sont caractérisés par une masse nulle, une vitesse égale à c (célérité de la lumière), une énergie E = hν, où ν est la fréquence de l'onde électromagnétique associée, et une quantité de mouvement avec où h désigne la constante de Planck et k le vecteur d'onde.

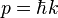
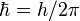
La théorie quantique de l'optique ou optique quantique a été créée pour concilier les deux aspects apparemment incompatibles de la lumière, l'aspect ondulatoire (phénomènes d'interférence, de diffraction ...) et l'aspect corpusculaire (effet photoélectrique, émission spontanée ...). L'optique quantique est essentiellement une reformulation de l'optique ondulatoire dans laquelle le champ électromagnétique est quantifié.

Avec l'optique quantique on abandonne toute certitude, on raisonne uniquement en termes de probabilités :

• probabilité qu'un photon soit émis ou absorbé par un atome ;
• probabilité qu'un photon émis par un atome ait une énergie donnée ;
• probabilité qu'un photon se désintègre ;
• ....