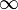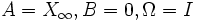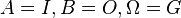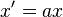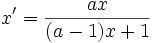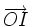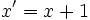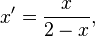Application projective - Définition

Homographies de la droite

Une bijection d'une droite projective dans elle-même est une homographie si et seulement si elle conserve le birapport. Donc si (A,B,C) et (A',B',C') sont deux triplets de points distincts de la droite, l'unique homographie qui transforme (A,B,C) en (A',B',C') est définie par

.

Nous rapportons la droite projective à un repère projectif , et rapportons au repère la droite affine obtenue en envoyant à l'infini le point  ; les coordonnées des différents points sont données dans le tableau :

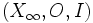
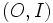
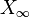
points		O	I	G
coordonnées homogènes	(1,0)	(0,1)	(1,1)	(1,2)
coordonnée affine		0	1	1/2

La classification des homographies de la droite provient de celle des matrices d'ordre 2 ; dans le cas où le polynôme caractéristique de l'application homogène est scindé (donc par exemple en géométrie complexe), il n'y a que deux possibilité, suivant que ce polynôme est à racines simples ou à une racine double :

Matrice homogène réduite dans un repère projectif (A,B,Ω)	Points fixes	cas	expression analytique dans ce cas	cas
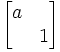
	A et B Homologie spéciale de base A et de centre B (ou l'inverse)	Homothétie de rapport a		Homographie à deux points fixes O et I
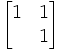
	A Homologie spéciale de base A et centre B	Translation de vecteur .		Homographie à un point fixe I

Dans le cas réel, les homographies à 2, 1 et 0 points fixes (correspondant à un discriminant de polynôme caractéristique >0, =0 ou <0) sont dites hyperboliques, parabolique, ou elliptiques.

Dans le cas complexe, les homographies de la droite projective complexe, qui est un plan réel adjoint d'un point à l'infini, et les homographies composées avec les réflexions (appelées antihomographies) forment exactement les transformations circulaires.

Liens

• Géométrie projective

• Fonction homographique

• Dualité (géométrie projective)

Caractérisation géométrique des homographies

On suppose dans ce paragraphe que et que les espaces sont de dimension finie.

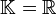
En dimension , les homographies d'un espace projectif dans lui-même sont les bijections transformant une droite en une droite, ou mieux, transformant trois points alignés en trois points alignés.

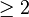
Ceci constitue le théorème fondamental de la géométrie projective, se déduisant du théorème fondamental de la géométrie affine. Il est remarquable qu'il n'y ait pas besoin de préciser la conservation du birapport dans cette caractérisation.