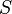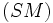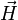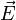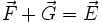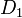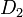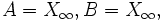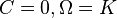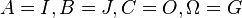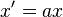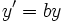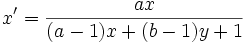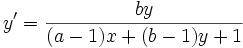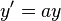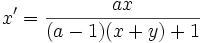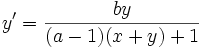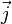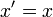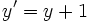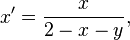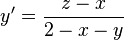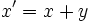Application projective - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Définition et premières propriétés - Expression analytique des applications projectives - Exemple des projections - Homographies du plan - Homographies de la droite - Liens - Caractérisation géométrique des homographies

Introduction

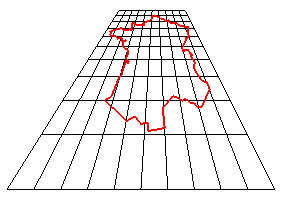
Une application projective est une application entre deux espaces projectifs qui préserve la structure projective, c'est-à-dire qui envoie les droites, plans, espaces,... en des droites, plans, espaces.

➪

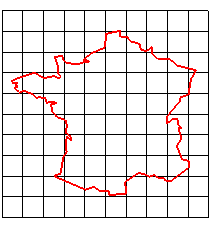Définition et premières propriétés

Rappelons que la définition moderne d'un espace projectif $E\,$ est d'être un ensemble dont les points sont les droites vectorielles d'un $\mathbb K$ -espace vectoriel $\vec E$ . 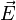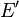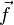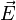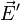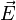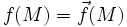Une application $f\,$ d'un espace projectif $E\,$ vers un espace projectif $E'\,$ est dite projective s'il existe une application linéaire $\vec f$ injective de $\vec E$ vers $\vec E'$ telle que pour tout point $M\,$ de $E\,$ (qui est aussi une droite de $\vec E$ ), $f(M)=\vec f(M)$ . L'application linéaire $\vec f$ , qui est définie à une constante multiplicative près, est appelée l'application homogène associée à $f\,$ (et $f\,$ est dite induite par $\vec f$ ).

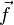
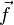
On peut généraliser au cas d'une application $\vec f$ non injective, mais alors l'application projective n'est plus définie que sur le complémentaire du sous-espace projectif de $E\,$ induit par le noyau de $\vec f$ .

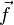
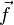
Si $E\,$ est de dimension $n\,$ , une application projective est entièrement déterminée par la donnée de $n+2\,$ points formant un repère projectif et de leurs images.

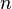
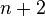
Les applications projectives transforment un sous-espace projectif en un sous-espace projectif, et conservent le birapport de 4 points alignés distincts.

Dans le cas $E=E'\,$ , les points fixes de $f\,$ ne sont autres que les droites de $\vec E$ dirigées par un vecteur propre de $\vec f$ associé à une valeur propre non nulle.

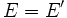
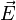
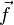
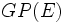
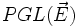
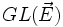
Les applications projectives bijectives sont appelées des transformations projectives, ou homographiques, ou encore des homographies. Les homographies d'un espace projectif dans lui-même forment un groupe, appelé le groupe projectif de $E\,$ , noté $GP(E)\,$ ; ce groupe, noté $PGL(\vec E)\,$ , est isomorphe au quotient de $GL(\vec E)\,$ par le sous-groupe des homothéties.

Une classe importante d'homographies est constitué par les homologies, ayant un hyperplan de points fixes, qui engendrent le groupe projectif en dimension finie.

Expression analytique des applications projectives

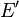
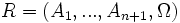
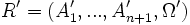
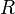
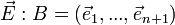
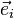
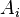
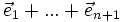
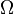
Nous rapportons les espaces projectifs $E\,$ et $E'\,$ à des repères projectifs $R=(A_1,...,A_{n+1},\Omega)\,$ et $R'=(A'_1,...,A'_{n+1},\Omega')\,$ ; pour $R\,$ , il existe une unique base de $\vec E : B=(\vec e_1,...,\vec e_{n+1})$ telle que $\vec e_i$ dirige $A_i\,$ et $\vec e_1+...+\vec e_{n+1}$ dirige $\Omega\,$ (idem pour $R'\,$ ).

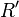
La matrice homogène de $f\,$ dans $R\,$ et $R'\,$ est la matrice $A=(a_{ij})\,$ de $\vec f$ dans $B\,$ et $B'\,$ .

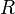
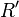
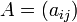
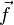
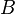
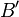
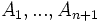
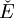
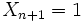
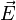
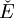
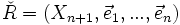
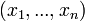
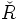
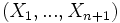
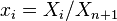
Si l'on envoie à l'infini l'hyperplan passant par $A_1,...,A_{n+1}\,$ , l'espace affine $\check E$ obtenu s'identifie à l'hyperplan $X_{n+1}=1\,$ de $\vec E$ et on rapporte $\check E$ au repère $\check R=(X_{n+1},\vec e_1,...,\vec e_n)$ ; les coordonnées affines $(x_1,..., x_n)\,$ d'un point $M\,$ dans $\check R$ et ses coordonnées homogènes $(X_1,...,X_{n+1})\,$ sont reliées par les relations $x_i=X_i / X_{n+1}\,$ . Si l'on fait de même dans $E'\,$ , l'expression analytique homogène de $f\,$ est donnée par les formules :

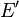
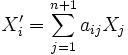
, et son expression analytique affine par les formules

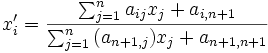
Les applications projectives sont donc définies analytiquement comme des quotients de formes affines par une même forme affine.

Exemple des projections

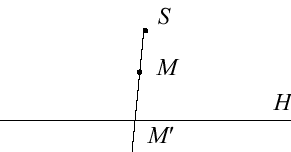Etant donné un hyperplan

de l'espace projectif

et un point

n'appartenant pas à

la projection (ou perspective) de centre

et de base

est l'application qui à tout point

différent de

fait correspondre le point d'intersection de la droite

avec

; c'est une application projective, car elle est induite par la projection vectorielle de base

(qui est un hyperplan de

) et de direction

(qui est une droite de

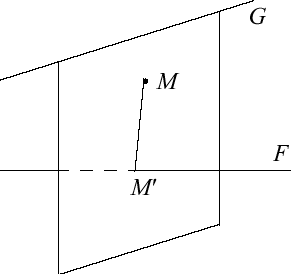Plus généralement, si

sont deux sous-espaces projectifs supplémentaires de

(c'est-à-dire

), la projection de sous-espace central

et de base

est l'application qui à tout point

n'appartenant pas à

fait correspondre le point d'intersection du sous-espace projectif engendré par

avec

. En dimension 3 par exemple, si

sont deux droites non coplanaires on peut définir la projection de droite centrale

et de base

Homographies du plan

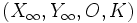
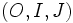
Nous rapportons le plan projectif à un repère projectif $(X_\infty,Y_\infty,O,K)$ , et rapportons à un repère $(O,I,J)\,$ le plan affine obtenu en envoyant à l'infini la droite $(X_\infty,Y_\infty)$ ; les coordonnées des différents points sont données dans le tableau :

points	$X_\infty$	$Y_\infty$	$O$	$I$	$J$	$K$	$G$
coordonnées homogènes	(1,0,0)	(0,1,0)	(0,0,1)	(1,0,1)	(0,1,1)	(1,1,1)	(1,1,3)
coordonnées affines	( $\infty$ ,0)	(0, $\infty$ )	(0,0)	(1,0)	(0,1)	(1,1)	(1/3,1/3)

La classification des homographies provient de celle des matrices d'ordre 3 ; pour les cas où le polynôme caractéristique de l'application homogène est scindé, on obtient :

Matrice homogène réduite dans un repère projectif $(A, B, C,Ω)$	Points fixes et droites stables	cas $A=X_\infty, B=X_\infty,$ $C=0,\Omega=K\,$	expressions analytiques dans ce cas	cas $A=I, B=J, C=O, \Omega=G\,$
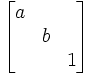
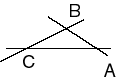$\begin{bmatrix} a & & \\ & b & \\ & & 1 \end{bmatrix}$		Biaffinité de rapport $a$ suivant $O x$ , et de rapport $b$ suivant $O y$	$x'=ax\,$ $y'=by\,$	$x'=\frac {ax} {(a-1)x+(b-1)y+1}$ $y'={by \over (a-1)x+(b-1)y+1}$
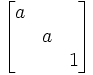
$\begin{bmatrix} a & & \\ & a & \\ & & 1 \end{bmatrix}$	La droite $(A B)$ est formée de points fixes, $C$ est fixe et les droites passant par $C$ sont stables.	Homothétie de rapport $a$ et de centre $O$	$x'=ax\,$ $y'=ay\,$	$x'=\frac {ax} {(a-1)(x+y)+1}$ $y'={by \over (a-1)(x+y)+1}$ Homologie générale de centre $O$ , de base $(I J)$ et de rapport $a$ .
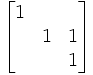
$\begin{bmatrix} 1 & & \\ & 1 & 1 \\ & & 1 \end{bmatrix}$	La droite $(A B)$ est formée de points fixes et les droites passant par $A$ sont stables	Translation de vecteur $\vec j$ .	$x'=x\,$ $y'=y+1\,$	$x'={x\over 2-x-y},$ $y'={z-x\over 2-x-y}\,$ Homologie spéciale de centre $I$ et de base $(I J)$
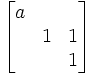
$\begin{bmatrix} a & & \\ & 1 & 1 \\ & & 1 \end{bmatrix}$	$A$ et $B$ sont fixes, et les droites $(A B)$ et ( $B C)$ sont fixes.	Dilatation de rapport $a$ suivant $O x$ et translation de vecteur $\vec j$ .	$x'=ax\,$ $y'=y+1\,$
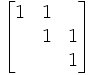
$\begin{bmatrix} 1 &1 & \\ & 1& 1 \\ & & 1 \end{bmatrix}$	$A$ est fixe et la droite $(A B)$ est invariante	Transvection suivant $O x$ et translation suivant $O y$	$x'=x+y\,$ $y'=y+1\,$

On peut remarquer qu'il y a toujours autant de points fixes que de droites stables. Plus généralement, on montre que pour toute homographie, il existe une dualité (bijection entre les points et les droites du plan inversant les appartenances) induisant une bijection entre ses points fixes et ses droites stables.

Homographies de la droite

Mars avait-elle un champ magnétique unilatéral ? 🔍

Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇

Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁

L'électroluminescence du graphène, une découverte inattendue ! 💡

Cet objet métallique n'a pas été fabriqué sur Terre 🔧

Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡

Cette super-Terre brûle les attentes des astronomes 🔥

Découverte exceptionnelle de fossiles d'amphibiens géants 🐸

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️

Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜

Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️

Cette vitamine développe les fonctions cognitives du cerveau 🧠

Comment des impacts géants vaporisent les corps planétaires ☄️

Les Américains riches vivent moins longtemps que les Européens pauvres 💰

Attention à ce riz naturellement riche en arsenic 🍚

L'intelligence artificielle contre la mort subite 💀

L'inévitable formation d'un océan de magma basal sur Terre 🔥

Découverte d'une plante étrange sans chlorophylle 🌱

Existe-t-il des mélodies naturelles ? 🎶

Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽

L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡

Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺

Imprimer en 3D avec la lumière du soleil ☀️

La pollution atmosphérique nuit gravement au cerveau 🧠

Le trou noir supermassif Ansky vient de se réveiller ⚫

Voici ce qui rend notre cerveau vraiment unique 🧠

Page générée en 0.155 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise