Codage binaire tronqué - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le codage binaire tronqué est un codage entropique utilisé essentiellement en compression de données et s'appuyant sur la base 2.
Il est plus généralement utilisé pour coder de façon efficace en termes de longueur, un alphabet dont la taille n'est pas une puissance de 2.
Principe
Contrairement au codage binaire de taille fixe, le codage binaire tronqué utilise un code préfixe à longueur variable. La longueur de ce code est toujours inférieure ou égale à celle du code binaire optimal équivalent, qui est de
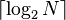
Pour un alphabet de taille N = 2k + b, le codage binaire tronqué sépare l'ensemble des valeurs à coder en deux groupes : les N − 2b = 2k − b = 2k + 1 − N premières valeurs d'une part, et les 2b valeurs restantes d'autre part. Les premières valeurs sont codées sur
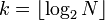
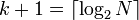
Les codes utilisés pour coder ces dernières valeurs sont les 2b derniers codes de longueur k + 1 ; il n'y a donc pas de continuité entre les valeurs codées sur k bits et celles codées sur k + 1 bits. C'est cette façon de coder qui fait du code binaire tronqué un code préfixe.
Exemples
Codage d'un alphabet de taille 5
Le code binaire optimal pour un alphabet de taille 5 est de longueur
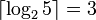
On peut donc coder sur 2 bits les 23 − 5 = 3 premières valeurs, et sur 3 bits les valeurs restantes.
| Décimal | Binaire optimal | Binaire tronqué |
|---|---|---|
| 0 | 000 | 00 |
| 1 | 001 | 01 |
| 2 | 010 | 10 |
| 3 | 011 | 110 |
| 4 | 100 | 111 |
Dans le cas d'une distribution uniforme, le codage binaire tronqué sur un alphabet de taille 5 offre un gain moyen de 0,6 bits par caractère, soit 20%.
Codage d'un alphabet de taille 7
Le code binaire optimal pour un alphabet de taille 7 est de longueur
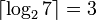
On peut donc coder sur 2 bits la 23 − 7 = 1 première valeur, et sur 3 bits les valeurs restantes.
| Décimal | Binaire optimal | Binaire tronqué |
|---|---|---|
| 0 | 000 | 00 |
| 1 | 001 | 010 |
| 2 | 010 | 011 |
| 3 | 011 | 100 |
| 4 | 100 | 101 |
| 5 | 101 | 110 |
| 6 | 110 | 111 |
Dans le cas d'une distribution uniforme, le codage binaire tronqué sur un alphabet de taille 7 offre un gain moyen de 0,14 bits par caractère, soit 4,76%.
Gains en termes d'espace par rapport au codage binaire
Dans le pire des cas, un code binaire tronqué est de la même longueur que le code binaire équivalent. Lorsque la taille de l'alphabet est une puissance de 2, ce pire cas est systématique, et les codes produits sont identiques. On peut ainsi voir le codage binaire comme un cas particulier de codage binaire tronqué, avec un alphabet dont la taille est une puissance de 2.
Dans tous les autres cas, le gain est de 1 bit pour chaque valeur parmi les
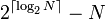
Le gain global G pour coder une source de longueur l sur un alphabet A de taille N peut être exprimé par :
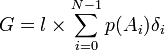
Où p(x) est la probabilité d'apparition de la valeur x et
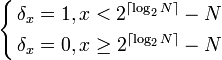
Lorsque la distribution des valeurs est connue et non uniforme, il est intéressant de réorganiser l'alphabet pour que les valeurs ayant la plus forte probabilité d'apparition soient au début de celui-ci.
Utilisations
Le codage binaire tronqué est utilisé pour coder un alphabet dont la taille n'est pas une puissance de 2, lorsque la longueur du code est critique. Dans le cas général (lorsque la vitesse est plus importante que la longueur du code), le codage binaire est préféré car il est plus simple et plus rapide à manipuler (notamment car sa taille fixe permet un indiçage immédiat).
Le codage binaire tronqué est en particulier utilisé pour le codage de la position lors d'un codage de Golomb ou d'un codage zeta.

















































