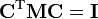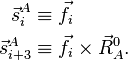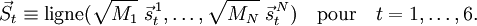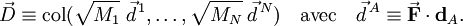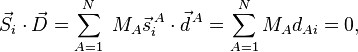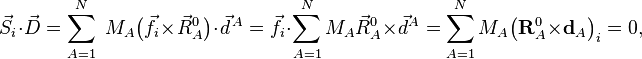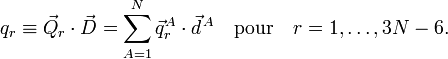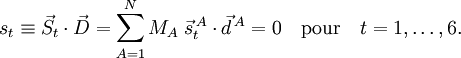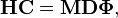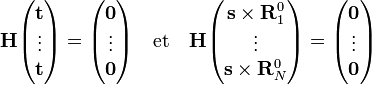Conditions d'Eckart - Définition
La liste des auteurs de cet article est disponible ici.
Séparation des coordonnées internes et externes
Les N vecteurs positions
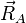
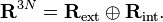
Afin de clarifier la nomenclature, on définit d'abord une base pour Rext. Pour cela on introduit les six vecteurs suivants (i = 1,2,3) :
Une base orthogonale, non normalisée, pour Rext est :
Un vecteur de déplacement pondéré peut alors être écrit :
Pour i=1,2,3,
où le zéro provient de l'application des conditions de translation d'Eckart. Pour i=4,5,6
où le zéro provient de l'application des conditions de rotation d'Eckart. On en déduit que le vecteur de déplacement
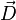
On obtient une base pour le sous-espace en définissant 3N-6 vecteurs linéairement indépendants :
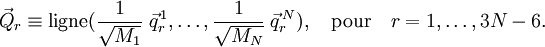
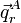
La signification physique de qr dépend des vecteurs
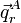
On a vu que les modes externes correspondants sont nuls en raison des conditions d'Eckart,
Relation à l'approximation harmonique
Dans l'approximation harmonique du problème de vibration nucléaire, exprimée en coordonnées de déplacement, on doit résoudre le problème le problème du polynôme de Jacobi :
où H est une matrice 3N x 3N symétrique des dérivées secondes du potentiel
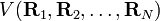
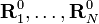
La matrice diagonale
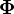
Donc, 6 colonnes de C correspondant à la valeur propre nulle, sont déterminés algébriquement. Si le problème généralisé des valeurs propres est résolu numériquement, on trouve généralement 6 combinaisons linéairement indépendantes de S et T). L'espace propre correspondant à la valeur propre nulle est au moins de dimension 6 (il est parfois exactement de dimension 6, qui sont les constantes de force, ne sont jamais nulles pour des molécules dans leur état fondamental). T et S correspondant alors aux mouvements externes (dans leur ensemble) : translation et rotation, respectivement. Ils sont les modes d'énergie nulle car l'espace est homogène (sans force) et isotrope (sans torsion).
Par définition, les modes de fréquence nulle sont des modes internes, appartenant au complémentaire orthogonal de Rext. Les orthogonalisations généralisées :