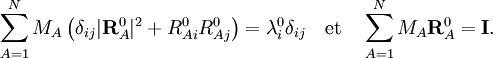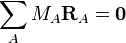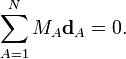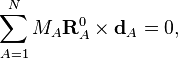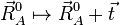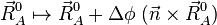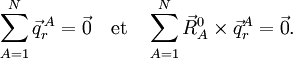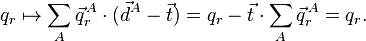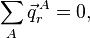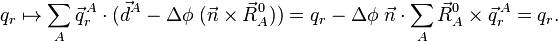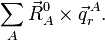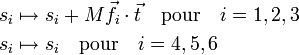Conditions d'Eckart - Définition

Introduction

Les conditions d'Eckart, nommées d'après le physicien américain Carl Eckart, et appelées parfois conditions de Sayvetz, permettent la simplification de l'équation de Schrödinger du mouvement nucléaire (rovibrationnel) lors de la seconde étape de l'approximation de Born-Oppenheimer. Les conditions d'Eckart permettent dans une large mesure la séparation des modes externes des modes internes. Bien que les mouvements de rotation et de vibration des noyaux dans une molécule ne puissent être complètement séparés, les conditions d'Eckart minimisent le couplage entre ces mouvements.

Définition des conditions d'Eckart

Les conditions d'Eckart peuvent seulement être formulées pour une molécule semi-rigide, qui est une molécule avec une surface d'énergie potentielle V(R₁, R₂,..R_N) possédant un minimum défini précisément pour R_A⁰ ( ). Ces coordonnées d'équilibre des noyaux - de masses M_A sont exprimées dans un repère à axes principaux orthonormés fixes et satisfont donc les relations :

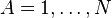
λ_i⁰ est ici un des moments d'inertie principaux de la molécule à l'équilibre. Les triplets R_A⁰ = (R_A1⁰, R_A2⁰, R_A3⁰) satisfaisant ces conditions, intègrent la théorie comme ensemble donné de constantes réelles. À l'instar de Biedenharn et Louck, on introduit un repère orthonormé fixe, le repère d'Eckart,

.

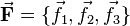
Si l'on est lié au repère d'Eckart, qui - suivant la molécule - tourne et translate dans l'espace, on observerait la molécule dans sa géométrie d'équilibre lorsque l'on fixe les noyaux à ces points

.

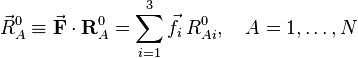
On choisit les éléments de R_A comme coordonnées dans le repère d'Eckart du vecteur position du noyau A ( ). Si l'on prend l'origine du repère d'Eckart au centre de masse instantané, les relations suivantes sont vérifiées :

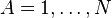
On définit alors les coordonnées de déplacement :

.

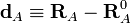
Ces coordonnées de déplacement satisfont les conditions de translation d'Eckart,

Les conditions de rotation d'Eckart pour les déplacements sont :

où indique un produit vectoriel.

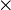
Ces conditions de rotation proviennent de la construction spécifique du repère d'Eckart (voir Biedenharn et Louck, loc. cit., page 538). Enfin, pour une meilleure compréhension du repère d'Eckart, il peut être utile de remarquer qu'il devient un repère selon les axes principaux dans le cas où la molécule est un rotateur rigide, soit lorsque les N vecteurs de déplacement sont nuls.

Translation et rotation globale

Les modes de vibration (internes) sont invariant par translation et rotation infinitésimale de la molécule à l'équilibre (référence) si et seulement si les conditions d'Eckart s'appliquent. Cela est démontré dans cette partie.

Une translation globale de la molécule de référence est donnée par :

pour un tri-vecteur abritraire.

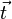
Une rotation infinitésimale de la molécule est décrite par :

où Δφ est un angle infinitésimal, Δφ >> (Δφ)², et est un vecteur unitaire arbitraire. L'orthogonalité de à l'espace externe implique que satisfasse :

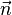
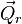
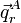
Maintenant, par translation :

Ainsi, est invariant par translation si et seulement si :

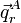
car le vecteur est arbitraire. Donc, les conditions sur les translations d'Eckart impliquent l'invariance transitionnelle des vecteurs appartenant à l'espace interne et inversement. Par rotation, on a :

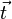
L'invariance par rotation s'ensuit si et seulement si :

Les modes externes, d'autre part, ne sont pas invariants et il n'est pas difficile de montrer qu'ils sont modifiés par translation comme ci-après :

où M est la masse totale de la molécule. Ils sont modifiés par rotation infinitésimale comme il suit :

où I⁰ est le tenseur d'inertie de la molécule à l'équilibre. Ce comportement indique que les trois premiers modes externes décrivent la translation d'ensemble et les trois derniers la rotation d'ensemble.