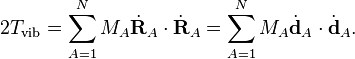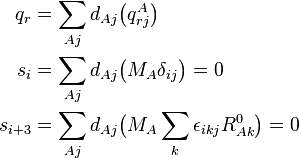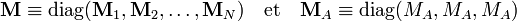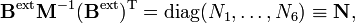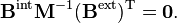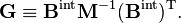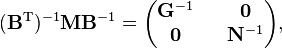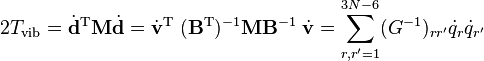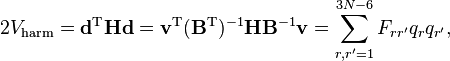Conditions d'Eckart - Définition

Énergie de vibration

L'énergie de vibration d'une molécule peut être écrite en termes de coordonnées par rapport au repère d'Eckart comme :

Le repère d'Eckart n'étant pas galiléen, l'énergie cinétique totale comprend aussi les termes de rotation et de Coriolis, que l'on considère comme implicites par la suite. L'énergie de vibration est écrite en termes de coordonnées de déplacment, qui sont linéairement dépendantes car influées par les 6 modes externes, nuls, i.e. les d_A satisfont à 6 relations linéaires. Il est possible d'écrire l'énergie de vibration uniquement en termes de modes internes q_r (r =1, ..., 3N-6) comme il va être montré par la suite. On écrit les différents modes en termes de déplacements

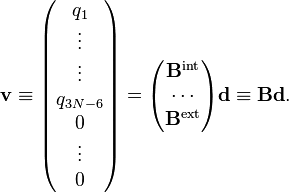
Les expressions entre parenthèses définissent une matrice B liant les modes internes et externes aux déplacements. la matrice B peut être divisée en une partie interne (3N-6 x 3N) et une partie externe (6 x 3N)

On définit la matrice M par :

et à partir des relations données précédemment on obtient les relations matricielles :

et

On définit

En utilisant les règles de multiplication des matrices par blocs, on montre que :

où G^-1 est de dimension (3N-6 x 3N-6) et N^-1 de dimension (6 x 6). Lénergie cinétique devient :

où les six derniers composants sont nuls. Cette forme de l'énergie cinétique de vibration fait partie de la méthode GF de Wilson. Il est intéressant de signaler que l'énergie potentielle dans l'approximation harmonique peut être écrite de la façon suivante :

où H est le hessien du potentiel au minimum et F, défini par cette équation, est la matrice F de la méthode GF.