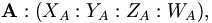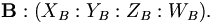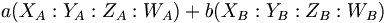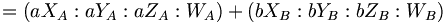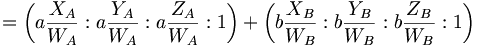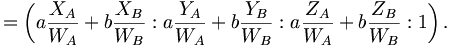Coordonnées homogènes - Définition

Combinaisons linéaires de vecteurs décrits avec les coordonnées homogènes

Prenons une paire de vecteurs A et B dans un espace en trois dimensions projectif, dont les coordonnées homogènes sont

On souhaite trouver leur combinaison linéaire où a et b sont des coefficients qui peuvent être ajustés à volonté. Il y a trois cas à considérer:

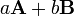
• les deux vecteurs dépendent d'un 3-espace affine,
• les deux vecteurs sont infinis,
• un vecteur est affine et l'autre est infini.

Les coordonnées X, Y, et Z peuvent être considérés comme numérateurs, W comme un dénominateur. Pour ajouter des coordonnées homogènes il est nécessaire que le dénominateur soit commun. Autrement il est nécessaire de redimensioner les coordonnées jusqu'à ce que tous les dénominateurs soient communs.

Les deux points sont affines

Si chacun des deux vecteurs est dans un 3-espace affine, alors et . Leur combinaison linéaire est

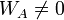
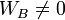
Les deux vecteurs sont infinis

Si chacun des deux vecteurs est infini, alors W_A = 0 et W_B = 0. Leur combinaison linéaire est

a(X_A:Y_A:Z_A:W_A) + b(X_B:Y_B:Z_B:W_B) = (aX_A:aY_A:aZ_A:0) + (bX_B:bY_B:bZ_B:0)

= (aX_A + bX_B:aY_A + bY_B:aZ_A + bZ_B:0).

Nous obtenons un autre vecteur infini.

Un vecteur est affine et l'autre est infini

Le premier vecteur est dans un 3-espace affine, donc . Alors

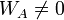
a(X_A:Y_A:Z_A:W_A) + b(X_B:Y_B:Z_B:0)

= a(0:0:0:0) + b(X_B:Y_B:Z_B:0),

= (bX_B:bY_B:bZ_B:0),

Nous obtenons un vecteur infini colinéaire au vecteur infini de la combinaison linéaire donc équivalent à ce dernier. Ceci signifie qu'un vecteur à l'infini est « dominant », en théorie des ensembles on dit que c'est un élément absorbant.