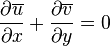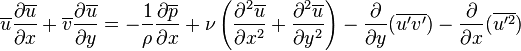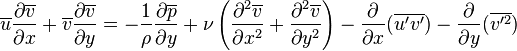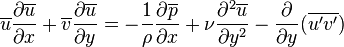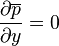Couche limite - Définition

Couche limite turbulente

Le traitement de la couche limite turbulente est plus difficile du à la dépendance du fluide à la variable temps. Une des technique les plus courante quand lequel le fluide est considéré comme turbulent, est d'appliquer la décomposition de Reynolds . Dans ce cas, les propriétés instantanées du fluide sont décomposées entre la moyenne et les fluctuations à la moyenne. En appliquant cette technique, les équations de la couche limite donnent une couche limite pleinement turbulente, qui ne sont pas souvent abordées dans la littérature :

En utilisant la même technique de calcul pour l'équation instantané, les équations deviennent dans sa forme classique :

Le terme additionnel dans la couche limite turbulente est connu sous le nom de contrainte partagé de Reynolds. La solution aux équations de la couche limite turbulente nécessite l'utilisation de modèle des turbulences, dont le but est d'exprimer la contrainte de Reynolds partagé dans des termes connu de variable du fluide et ses dérivés. Le manque de précision et la non généralisation de ces modèles est l'obstacle majeur dans le succès des prédictions des propriétés des écoulements turbulents dans la science de la dynamique des fluides.

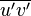
Bibliographie

• (en) A.D. Polyanin, A.M. Kutepov, A.V. Vyazmin et D.A. Kazenin, Hydrodynamics, Mass and Heat Transfer in Chemical Engineering, Taylor & Francis, London, 2002. ISBN 0-415-27237-8
• (en) Herrmann Schlichting, Klaus Gersten, E. Krause, H. Jr. Oertel, C. Mayes Boundary-Layer Theory 8th edition Springer 2004 ISBN 3-540-66270-7
• (en) John D. Anderson, Jr, Ludwig Prandtl's Boundary Layer, Physics Today, December 2005