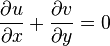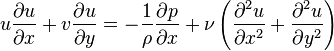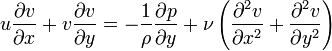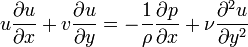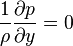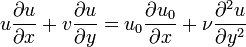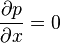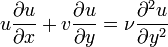Couche limite - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La couche limite est la zone d'interface entre un corps et le fluide environnant lors d'un mouvement relatif entre les deux, conséquence de sa viscosité. Elle est un élément important en mécanique des fluides, (aérodynamique, hydrodynamique), en météorologie, en océanographie, etc.
Description
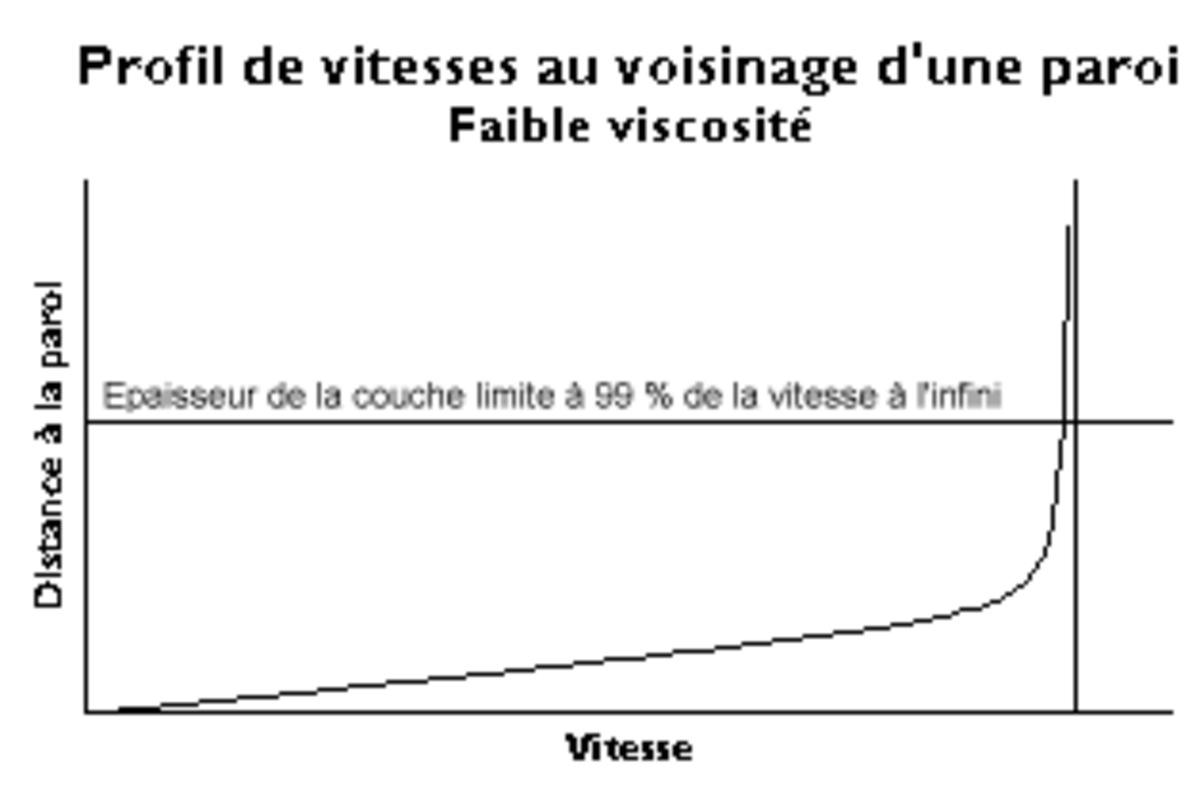
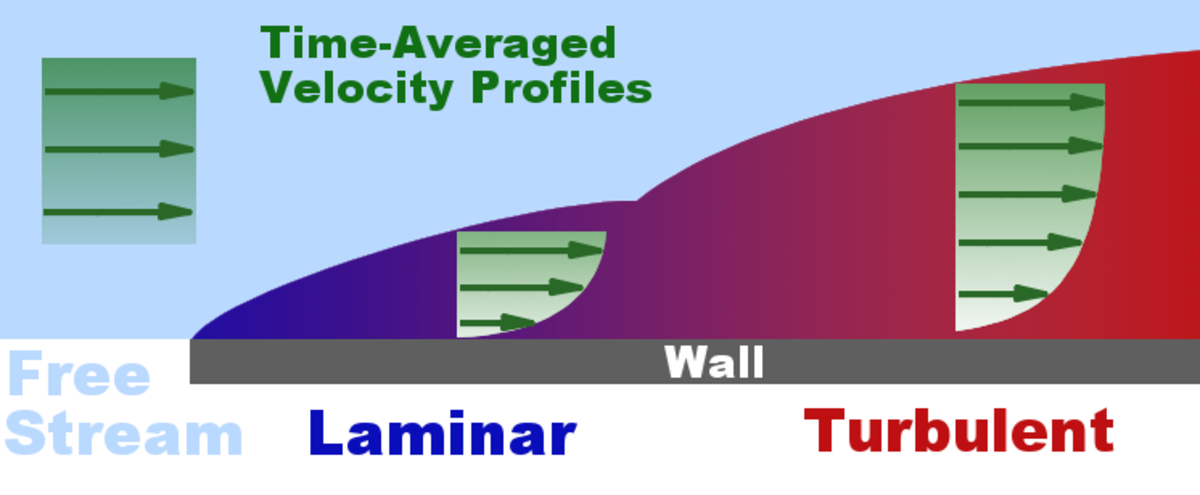
Lorsqu'un fluide réel s'écoule le long d'une paroi supposée fixe, les vitesses sur la paroi sont nulles et à l'infini, loin de l'obstacle, elles sont égales à la vitesse de l'écoulement non perturbé. Sur une normale à la paroi la vitesse doit donc dans tous les cas varier entre 0 et un maximum. La loi de variation dépend de la viscosité du fluide qui induit un frottement entre les couches voisines : la couche la plus lente tend à freiner la couche la plus rapide qui, en retour, tend à l'accélérer.
Dans ces conditions, une forte viscosité égalise au maximum les vitesses. Au contraire, si le fluide est peu visqueux, les différentes couches sont beaucoup plus indépendantes : la vitesse à l'infini se maintient jusqu'à une courte distance de l'obstacle et il y a une variation plus forte des vitesses dans la petite épaisseur de la couche limite.
Dans le premier cas, il faut utiliser les équations générales du fluide visqueux. Dans le second, on peut utiliser dans la couche limite des équations simplifiées complétées par des résultats expérimentaux. Les équations, également plus simples, du fluide parfait appliquées au-delà de la paroi « engraissée » par la couche limite fournissent les conditions aux limites pour le calcul.
En fait, ce n'est pas la viscosité elle-même qui intervient. Comme toujours en mécanique des fluides, c'est un nombre sans dimension qui caractérise le phénomène : le nombre de Reynolds. Celui-ci décrit le rapport des forces liées à la vitesse aux forces de frottement. Ainsi, au lieu d'augmenter la viscosité, on peut obtenir un phénomène semblable en diminuant la vitesse ou les dimensions de l'obstacle.
Équations de la couche limite
La compréhension et la modélisation des équations de la couche limite sont peut être une des plus importantes avancées de la dynamique des fluides. En utilisant Analyse d'échelle, les Équations de Navier-Stokes peuvent être écrites sous forme simplifiée. En effet, les Équations de Navier-Stokes originales sont elliptiques alors que les équations simplifiées sont paraboliques. Cela simplifie grandement la résolution des équations. La simplification repose sur la division en deux de l'espace dans lequel s'écoule le fluide : la couche limite et le reste de l'espace (le reste étant facile à résoudre par de nombreuses méthodes). La couche limite est alors gouvernée par des équations différentielles partielles faciles à résoudre. Les Équations de Navier-Stokes et de continuité pour un écoulement bidimensionnel incompressible en coordonnées cartésiennes sont :
où u et v sont les composantes de la vitesse, ρ est la masse volumique, p la pression, et ν est Viscosité cinématique du fluide en un point.
Un écoulement qui a un nombre de Reynolds élevé peut être simplifié. La simplification consiste à diviser l'espace en deux régions. La première est la région où l'écoulement du fluide n'est pas affecté par la viscosité (la majorité de l'espace), l'autre région - proche des surfaces du domaine - est la région ou la viscosité joue un rôle important (couche limite). Alors u et v sont respectivement la vitesse sur la ligne de courant et la vitesse normale à la ligne de courant à l'intérieur de la couche limite. En utilisant l'analyse d'échelle, les équations de mouvement pour la couche limite se simplifient et deviennent :
et si le fluide est incompressible (cas d'un liquide dans les conditions standards) :
Une analyse asymptotique montre que v, la vitesse normale est petite comparée à u la vitesse sur une ligne de courant, et que les propriétés de ses variations dans la direction de la ligne de courant sont généralement moins importantes que dans la direction normale.
La pression statique p est indépendante de y, alors la pression au bord de la couche limite est la pression de la ligne de courant. La pression externe peut être calculée en appliquant le Théorème de Bernoulli. Alors u0 est la vitesse du fluide en dehors de la couche limite, où u et u0 sont parallèles. En remplaçant p, les équations sont :
avec les conditions limites
Pour un fluide dans lequel la pression statique p ne dépend pas de la direction d'écoulement du fluide :
donc u0 reste constant.
Les équations de mouvement simplifiées sont :
Ces approximations sont utilisées dans un grand nombre de problèmes scientifiques et d'ingénierie. L'analyse précédente est pour toute couche limite (laminaire ou turbulente), mais les équations sont principalement utilisées pour étudier la couche limite laminaire. En effet la moyenne de la vitesse correspond à la vitesse instantanée car il n'y a pas la présence de fluctuations de vitesses.