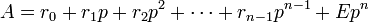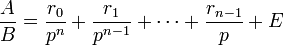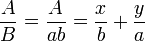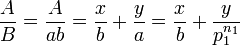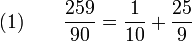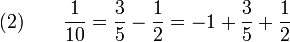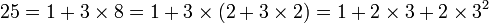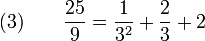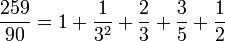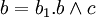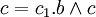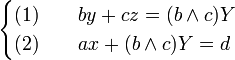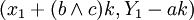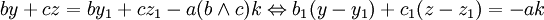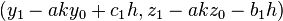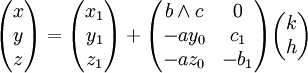Équation diophantienne ax+by = c - Définition

Recherche de solutions dans l'ensemble des entiers naturels

On ne considère ici que la résolution de l'équation ax + by = c où a, b, c sont des entiers naturels, a et b premiers entre eux, les solutions étant cherchées parmi les entiers naturels. Lucas attribue à Paoli et Cesàro les deux résultats suivants:

Si l'on s'intéresse alors plus précisément aux entiers r compris entre 0 et ab - 1, pour lesquels l'équation ax + by = r admet une solution; on peut démontrer que

• Si r est multiple de a ou de b l'équation comporte une unique solution;
• Si r est inférieur à a + b et n'est multiple ni de a ni de b, l'équation ne comporte pas de solution;
• Parmi les équations ax + by = r et ax + by = ab - r où r n'est ni multiple de b ni multiple de a, une seule d'entre elles possède une solution entière positive.

On en déduit le nombre d'entiers r compris entre 0 et ab - 1 pour lesquels l'équation ax + by = r admet une solution.

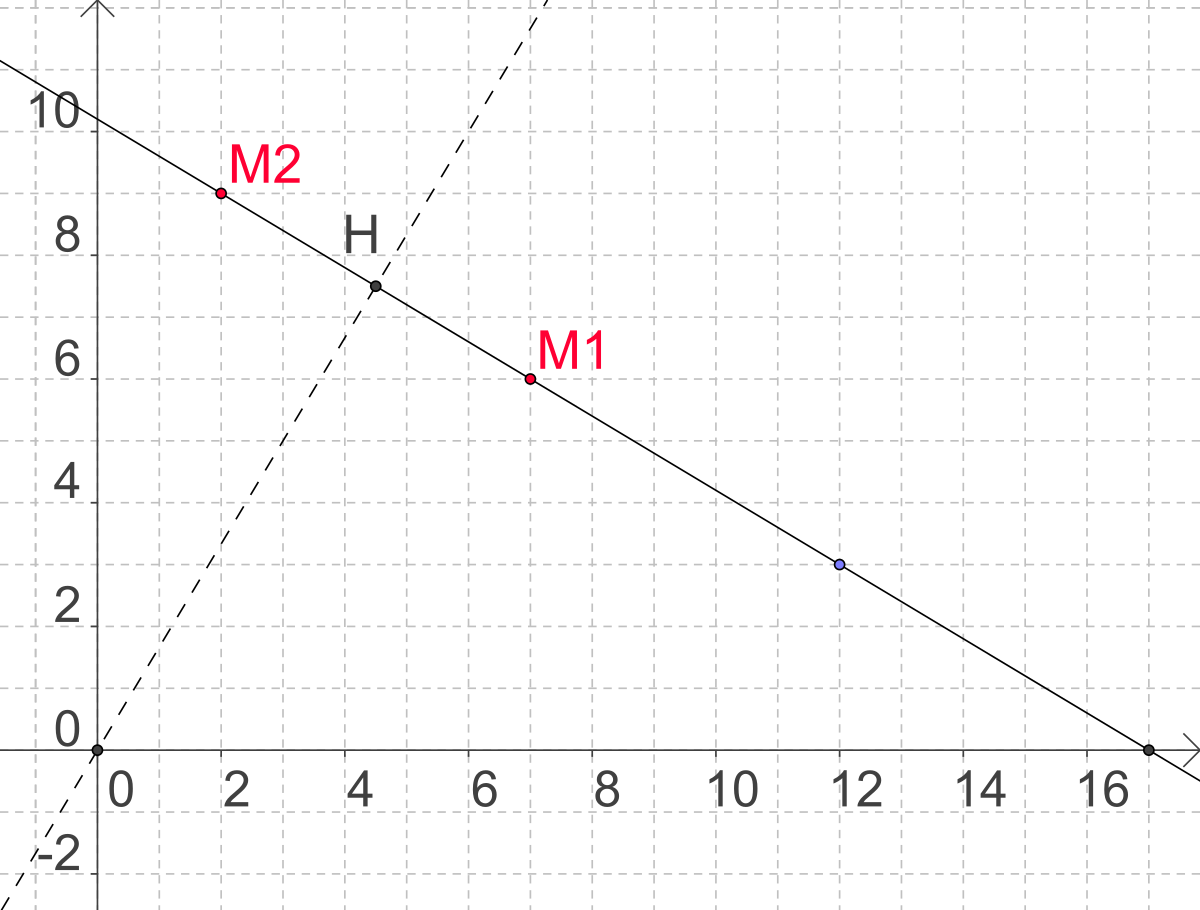
Lorsque un entier r compris entre 1 et ab - 1 est donné, pour déterminer si l'équation ax+by = r admet une solution il faut observer le système minimal. Le point de la droite ax + by = r le plus proche de l'origine est de coordonnées rationnelles positives.

L'unique solution entière positive (si elle existe) de l'équation ax + by = r correspond à un des points de la droite à coordonnées entières les plus proches de ce point. Si (x₁,y₁) est une solution dans l'ensemble des entiers relatifs de l'équation ax + by = r, l'unique solution positive (si elle existe) de l'équation est donc à chercher dans les deux couples (x₁ + bk₁,y₁ − ak₁) ou (x₁ + bk₂,y₁ − ak₂) où k₁ et k₂ sont les deux entiers les plus proches de . Si aucun de ces deux couples n'est dans , l'équation n'admet pas de solution.

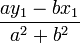
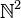
Applications

Congruence

La résolution de l'équation ax + by = 1, où a et b sont premiers entre eux, permet de trouver un inverse à a modulo b, c'est-à-dire un entier x tel que .L'ensemble des solutions permet de dire qu'il existe une unique classe x tel que ax=1 dans . En effet, parmi les couples solutions, tous les entiers x sont congrus modulo b.

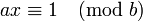
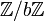
Équation de droite

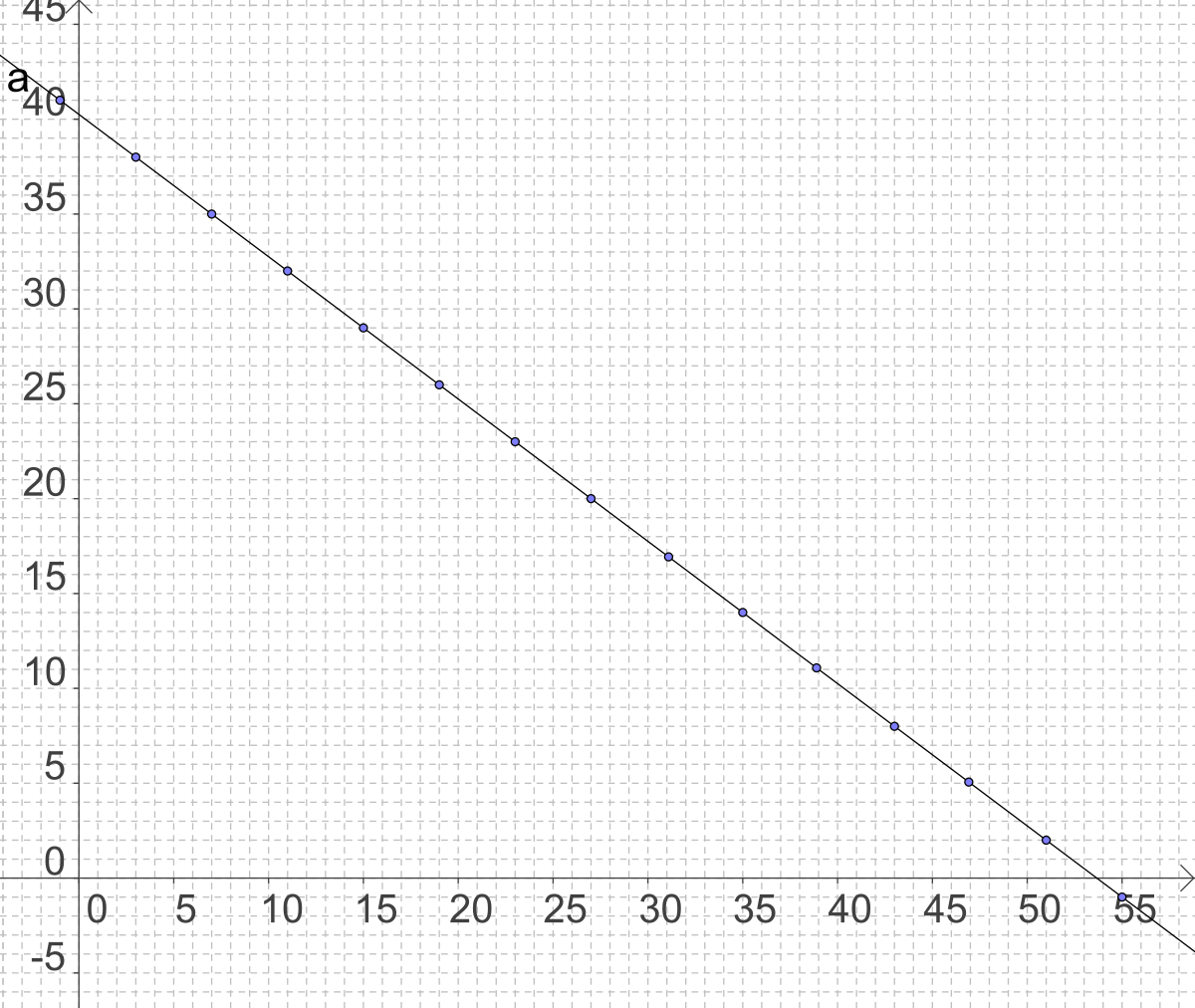
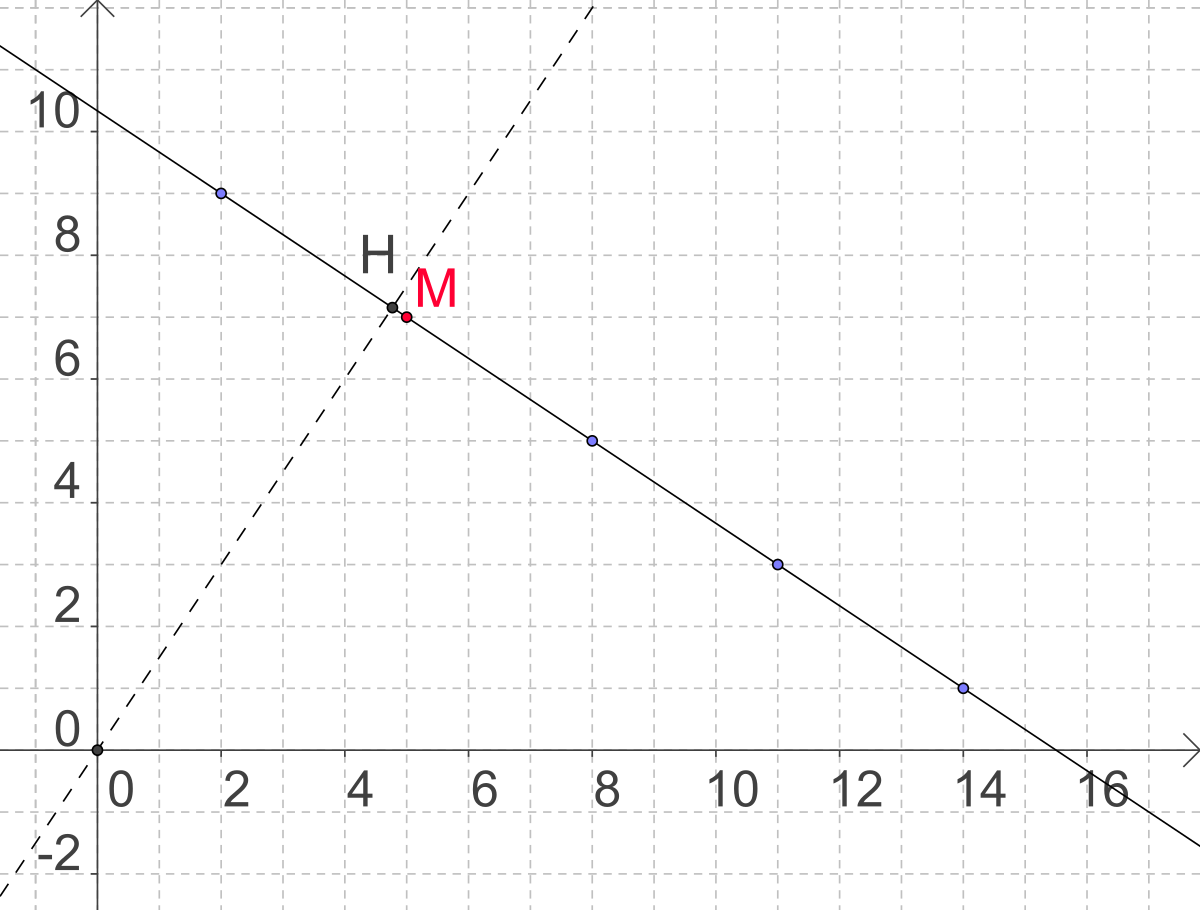
L'ensemble des points M(x , y) vérifiant l'équation ax + by = c forme une droite. Les couples d'entiers relatifs vérifiant cette équation correspond aux points M de la droite dont les coordonnées sont entières. La résolution de l'équation dans l'ensemble des entiers relatifs permet de donner les coordonnées de ces points. Selon la valeur de c, la droite D peut ne jamais passer par des points de coordonnées entières ou bien posséder une infinité de points de coordonnées entière régulièrement répartis.

Résolution graphique de l'équation 9x + 12y = 483

La droite d'équation 4x + 6y = 81 ne passe par aucun point de coordonnées entières

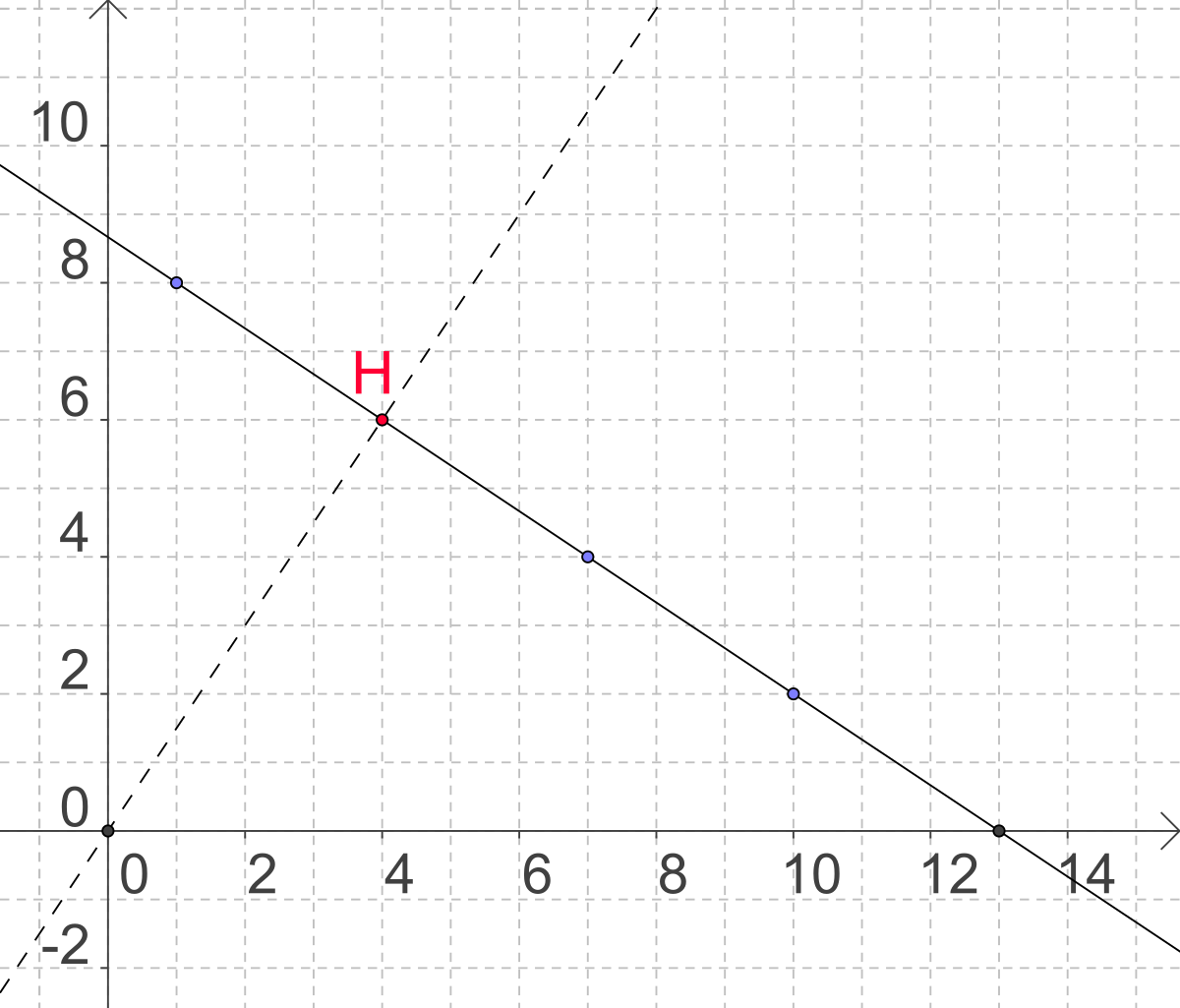
La solution du système minimal se lit alors très facilement. Le ou les couples solutions correspondent aux points dont les coordonnées vérifient x² + y² est minimal. Ce sont donc les points de la droite les plus proches de l'origine. Le point O se projette sur la droite en H. La solution du système minimal est donc le (ou les) points de la droite de coordonnées entières situé(s) le plus près de H.

Les coordonnées de H fournissent la solution au système minimum de l'équation 2x +3y = 26

Les coordonnées de M1 et M2 fournissent les solutions au système minimum de l'équation 3x + 5y = 51

Les coordonnées de M fournissent la solution au système minimum de l'équation 2x + 3y = 31

Réduction d'une fraction en éléments simples

Décomposer une fraction irréductible en éléments simples , c'est la décomposer en somme d'un entier relatif et de fractions de la forme dans laquelle p_i est un nombre premier apparaissant dans la décomposition de B en facteurs premiers, j est un exposant entier non nul ne dépassant pas l'exposant de p_i dans la décomposition de B et r_j,i est un entier compris entre 0 et p_i − 1.

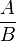
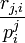
Lucas prouve l'existence d'une telle décomposition. Il procède en plusieurs étapes.

Si B = pⁿ, où p est un nombre premier, une simple écriture de A dans la base p permet d'aboutir. En effet

où les r_i sont des entiers compris entre 0 et p - 1 et E est un entier relatif. D'où en divisant par B

La seconde étape consiste à travailler sur un nombre B = ab où a et b sont premiers entre eux et c'est là qu'intervient l'équation diophantienne. Les deux nombres sont premiers entre eux, il existe donc des entiers relatifs x et y tels que

ax+by = A

donc

La décomposition de la fraction sera donc établie dès que seront obtenues les décompositions des fractions x/b et y/a.

Lucas procède alors de proche en proche. Si alors on peut poser et

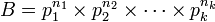
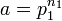
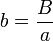
La seconde fraction se décompose aisément et la première est à décomposer en utilisant le même processus. Il suffit de k-1 étapes pour arriver au bout de la décomposition complète.

Lucas démontre que malgré la multiplicité des méthodes pour arriver à la décomposition, celle-ci est unique.

Exemple : Décomposition de la fraction

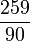
On décompose 90 en 9 × 10. On cherche deux entiers x et y tels que 9x + 10y = 259. On peut prendre x=1 et y=25.

On décompose 10 en 2 ×5. On cherche deux entiers x et y tels que 2x + 5y = 1. On peut prendre x = 3 et y = - 1.

On écrit 25 en base 3

Donc

Il suffit de remplacer dans (1) les résultats trouvés dans (2) et (3)

Généralisation aux dimensions supérieures

Les techniques mises en place pour la résolution de l'équation ax + by = c peuvent être réinvesties pour la résolution des équations linéaires à plus d'inconnues. En particulier, elles permettent de résoudre l'équation diophantienne linéaire ax + by + cz = d.

Comme dans le cas de la dimension 2, on peut remarquer que l'équation n'admet pas de solution si d n'est pas un multiple du PGCD de (a, b, c). Si d est multiple du PGCD, on peut diviser chacun des coefficients par le PGCD, on se ramène alors à une équation du même type dans lequel les coefficients devant x, y, et z sont premiers entre eux dans leur ensemble.

Dans l'équation ax + by + cz = d, où a, b, c sont premiers entre eux, on pose le PGCD de b et c et note b₁ et c₁ les entiers relatifs, premiers entre eux tels que

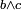
by + cz étant toujours un multiple de , l'équation est équivalente au système

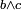
Les entiers a et étant premiers entre eux, la seconde équation admet des solutions et, pour tout Y la première équation admet des solutions. L'équation ax + by + cz = d admet donc toujours des solutions.

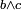
Si on appelle (x₁,y₁,z₁) l'une d'entre elle et (y₀,z₀) une solution de l'équation b₁y + c₁z = 1. On peut noter .

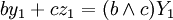
Les solutions de l'équation (2) sont les couples :

où k est un entier relatif quelconque

L'équation (1) s'écrit alors :

dont les solutions sont les couples :

où h est un entier relatif quelconque.

Les solutions de l'équation de départ sont donc données par l'égalité matricielle suivante

où h et k sont des entiers relatifs quelconques.