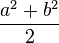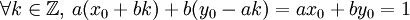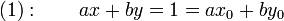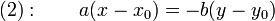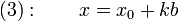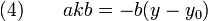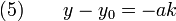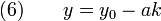Équation diophantienne ax+by = c - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L'équation ax + by = c, où les coefficients a, b, et c, sont trois entiers relatifs et où les inconnues x et y sont entiers relatifs, est une des équations diophantiennes les plus simples à résoudre. Sa résolution s'appuie sur l'algorithme d'Euclide, le théorème de Bachet-Bézout et le théorème de Gauss. Lorsque c est égal au PGCD de a et b, on parle parfois d’identité de Bézout.
Dans l'ensemble des entiers relatifs, une telle équation possède, ou bien aucune solution, ou bien une infinité de solutions. Lorsque les coefficients et les inconnues sont des entiers naturels, l'équation possède un nombre fini de solutions. Le théorème de Paoli en donne le nombre à 1 près.
Recherche de solutions dans l'ensemble des entiers relatifs
Équation ax + by = 1 où a et b sont premiers entre eux
Le théorème de Bachet-Bézout affirme que cette équation admet toujours au moins une solution.
La première étape de la résolution consiste à trouver une solution particulière , c'est-à-dire un couple d'entiers relatifs (x0, y0) vérifiant : ax0 + by0 = 1.
- L'algorithme d'Euclide étendu permet d'en exhiber une.
- Une autre méthode consiste à utiliser le développement en fraction continue de a/b, l'avant dernière réduite fournit une solution du problème: Si
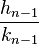
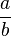
- Mais on peut aussi, si b n'est pas trop grand, chercher une solution par simple balayage en travaillant modulo b et en cherchant un entier x0 compris entre 1 et |b| - 1, vérifiant
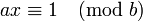
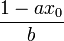
Ensemble des solutions — Une solution particulière (x0, y0) étant connue, l'ensemble des solutions est formée des couples (x0+bk, y0 - ak) où k est un entier relatif quelconque.
En effet, il est facile de vérifier qu'un tel couple est solution du problème :
Il s'agit maintenant de prouver que seuls ces couples sont solutions. Supposons donc que le couple (x ,y) est solution de l'équation. On a donc
En regoupant autrement les termes, on obtient
L'entier b divise donc le produit a(x - x0). Comme a et b sont premiers entre eux, le lemme de Gauss permet de dire que b divise x - x0. Il existe donc un entier relatif k tel que x - x0 = kb. Soit encore
En remplaçant x - x0 par kb dans (2) on obtient :
Puis en simplifiant par -b
Soit encore
Donc, si (x,y) est solution de (1) alors, il existe un entier relatif k tel que (x,y) = (x0+bk, y0 - ak)
Équation ax + by = c où a et b sont premiers entre eux
Une solution particulière peut être trouvée en multipliant par c une solution particulière de l'équation ax + by = 1. En effet, si (x0, y0) vérifie ax0 + by0 = 1 alors ax0c + by0c = c, le couple (x0c, y0c) est alors solution de l'équation ax + by = c.
Un raisonnement analogue au précédent permet de trouver l'ensemble des solutions :
Ensemble des solutions — Une solution particulière (x1, y1) étant connue, l'ensemble des solutions est formé des couples (x1+bk, y1 - ak) où k est un entier relatif quelconque.
Cas général
On appelle d le pgcd de a et de b.
Si c n'est pas un multiple de d — L'équation n'a pas de solution.
En effet, d divisant a et b, d divise aussi toute expression de la forme ax + by où a et b sont des entiers relatifs, donc d doit diviser c
On suppose maintenant que d divise c, il existe alors 3 entiers relatifs a1, b1, et c1 tels que
- a = da1
- b = db1
- c = dc1
avec a1et b1 premiers entre eux.
L'équation ax + by = c est alors équivalente à l'équation a1x + b1y = c1 dans laquelle a1 et b1 sont premiers entre eux, et ce cas a déjà été résolu. On obtient alors la résolution dans le cas général :
- Une solution particulière (x1, y1) étant connue, l'ensemble des solutions est formé des couples (x1+b1k, y1 - a1k) où k est un entier relatif quelconque.
D'où la propriété :
Si c est un multiple de d — L'équation admet toujours des solutions. Une solution particulière (x1, y1) étant connue, l'ensemble des solutions est formé des couples
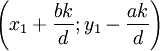
Système minimal
On suppose dans cette section que c est un multiple de d. Parmi toutes les solutions d'une équation ax + by = c donnée, on peut chercher celle(s) pour laquelle x2 + y2 soit la plus petite possible.
Il s'agit de rendre minimal la valeur (x1 + b1k)2 + (y1 − a1k)2. Si on considère la fonction de la variable réelle t définie parf(t) = (x1 + b1t)2 + (y1 − a1t)2, l'étude de cette fonction du second degré montre que celle-ci possède un minimum en
Si t est entier, le couple solution est alors (x1 + b1t,y1 − a1t), sinon, l'entier qui rend f minimal est le (ou les) entier(s) k le(s) plus proche(s) de t.
Le(s) couple(s) d'entiers solution de ax + by = c dont la valeurx2 + y2 est minimale sont le (ou les) couple(s) (x1 + b1k,y1 − a1k) où k est le (ou les) entier(s) k le(s) plus proche(s) de
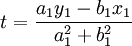
Dans le cas où a et b sont premier entre eux, le cas où t est entier mérite d'être explicité. On démontre que t est entier si et seulement si l'entier c est un multiple dea2 + b2. La solution du système minimal est alors
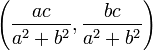
Dans le cas où a et b sont premiers entre eux, il existe deux solutions au système minimal si et seulement si a et b sont impairs et l'entier c est un multiple impair de