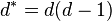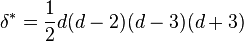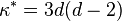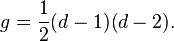Formule de Plücker - Définition

Exemples et applications

Nombre maximum de points doubles

Pour une courbe (non dégénérée) de degré d, sans points de rebroussement, et admettant δ points doubles, on a un genre g égal à (d-1)(d-2)/2-δ ; comme il doit être positif, on en déduit qu'on a au maximum (d-1)(d-2)/2 points doubles ; ce maximum est effectivement atteint pour les courbes unicursales, de genre 0. Plus généralement, s'il y a κ points de rebroussement, les différentes formules imposent des maximums à δ, mais il n'est pas toujours aussi simple de voir s'ils sont effectivement atteignables. Ainsi, par exemple, pour d = 7 et κ = 8, on a respectivement d^* = 18 - 2δ, donc (puisque d^* > 3, comme on le verra ci-dessous) δ < 8 ; κ^* = 41 - 6δ, donc δ < 7, et enfin g = 7 - δ, donc δ < 8 ; on a donc au maximum 6 points doubles dans ce cas, et de plus g vaut au moins 1, d^* au moins 6, et C possède au moins cinq points d'inflexion.

Courbes non singulières

Un cas particulier important est celui où C, de degré d, est régulière, ce qui équivaut à δ = κ = 0 ; les autres invariants peuvent alors être obtenus à l'aide de d uniquement. Dans ce cas, on trouve :

Ainsi, par exemple, une quartique (en) (une courbe de degré 4) régulière est de genre 3 et possède 28 bitangentes et 24 points d'inflexion.

Cubiques

Une cubique (d=3) ayant deux points singuliers est dégénérée (elle est réunion d'une droite et d'une conique) ; on peut le démontrer à l'aide de la deuxième formule de Plücker : on aurait en effet alors κ^* inférieur à 9-12 < 0, ce qui est absurde. Les seuls cas possibles non dégénérés sont donc les cubiques régulières (δ = κ = 0), les cubiques admettant un point double (δ = 1, κ = 0), et les cubiques admettant un point de rebroussement (δ = 0, κ = 1).

Dans le cas des cubiques régulières, pour lesquelles le genre vaut 1, on a d^* = 6 (par tout point du plan passent donc six tangentes à la courbe), δ^* = 0 (il n'y a pas de bitangentes) et κ^* = 9 ; il y a donc neuf points d'inflexion (mais trois d'entre eux au plus sont réels), sur lesquels on trouvera plus de détails à l'article courbe elliptique.

Les cubiques admettant un point double ont une courbe duale plus simple : on a pour elles d^* = 4 et κ^* = 3. Utilisant la troisième formule de Plücker, on aura donc 2δ^* = 12-9-3 = 0, et finalement g = 0 : ce sont des cubiques unicursales, parmi lesquelles figurent les strophoïdes.

Enfin, les cubiques à point de rebroussement sont les cissoïdes (elles aussi unicursales), pour lesquelles d^* = 3 et κ^* = 1 ; leur courbe duale est donc également une cubique à point de rebroussement.