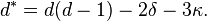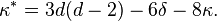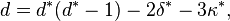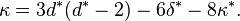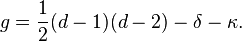Formule de Plücker - Définition

Introduction

En mathématiques, et plus précisément en géométrie algébrique, une formule de Plücker est une relation entre certains invariants numériques de courbes algébriques, tels que le nombre de leurs points critiques, et les invariants correspondants de leurs courbes duales ; les premiers exemples de ces formules furent découverts par Julius Plücker vers 1830. Le genre, un invariant commun à une courbe et à son dual, est lié aux autres invariants par des formules similaires. Comme ces invariants sont des entiers positifs, ces formules donnent des limites assez strictes à leurs valeurs possibles.

Invariants de Plücker et équations fondamentales

Courbes duales l'une de l'autre.

Les courbes auxquelles s'appliquent les formules de Plücker sont celles définies dans le plan projectif complexe par une équation algébrique non dégénérée (c'est-à-dire que l'équation ne se factorise pas, et donc que la courbe n'est pas réunion de deux courbes plus simples). Les droites de ce plan correspondent aux points du plan projectif dual, et les tangentes à une courbe algébrique donnée C correspondent aux points d'une courbe algébrique C^* appelée la courbe duale de C. Les points de C correspondent alors aux tangentes à C^*, et la courbe duale de C^* peut donc être identifiée avec C.

Les deux premiers invariants reliés par les formules de Plücker sont le degré d de la courbe C et le degré d^* de son dual, traditionnellement appelé la classe de C. Géométriquement, d est le nombre d'intersections d'une droite donnée avec C, en comptant les points complexes et les points à l'infini, et en prenant aussi en compte la multiplicité des intersections ; de même, d^* est le nombre de tangentes à C passant par un point donné du plan. Ainsi, par exemple, une conique est de degré et de classe 2. Si C n'a pas de singularités, la première formule de Plücker dit que

,

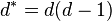
mais des termes correctifs doivent être ajoutés pour prendre en compte les singularités, comme on va le voir.

Parmi les points doubles de C, soit δ le nombre de ceux qui sont ordinaires, c'est-à-dire qui ont des tangentes (éventuellement complexes) distinctes, et soit κ le nombre des points de rebroussement (si C possède des singularités d'ordre plus élevé, il faut les compter comme des points doubles "multiples" ; par exemple, un point triple ordinaire sera compté comme 3 points doubles, mais les formules de Plücker généralisées correspondantes ne seront pas détaillées ici). Là encore, les points complexes et à l'infini doivent être pris en compte. La forme complète de la première formule de Plücker est alors :

De même, soit δ^* le nombre de points doubles (ordinaires) et κ^* le nombre de points de rebroussement de C^*. Alors la deuxième formule de Plücker est :

L'interprétation géométrique d'un point double ordinaire de C^* est d'être une droite bitangente à C (une tangente à C en deux points distincts) et celle d'un point de rebroussement de C^* est d'être une tangente "stationnaire", c'est-à-dire une tangente d'inflexion de C.

Ces deux relations sont également vraies pour C^*, et donc :

Les quatre formules précédentes sont en fait liées : trois d'entre elles permettent de déduire la quatrième. Elles permettent, étant donnés trois des six invariants d, d^*, δ, δ^*, κ et κ^*, de calculer les trois autres.

Enfin, le genre (géométrique) de C (connu historiquement sous le nom de déficience de C) peut être défini par :

C'est un entier positif, égal à la quantité duale

 ;

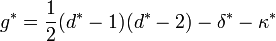
dans le cas où C n'a pas de points singuliers, on obtient la formule classique g = (d − 1)(d − 2)/2. Cet ensemble de relations entre les sept invariants permet, en connaissant trois quelconques d'entre eux, de calculer les quatre autres.