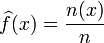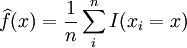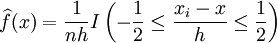Histogramme - Définition

Origine

William Playfair (Commercial and political atlas, 1786) est le premier promoteur de l'exploitation des observations statistiques par des courbes de distribution et des diagrammes en bâtons. Le mot histogramme a été proposé par Pearson en 1895.

Un outil pour estimer une densité

Dans cette section, on utilise l'histogramme non pas comme un outil de visualisation, mais comme une estimation statistique de la distribution sous-jacente de l'échantillon. On dispose d'un échantillon indépendamment et identiquement distribué selon une loi. On souhaite déduire de l'échantillon une estimation de la densité inconnue, notée f.

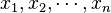
Le cas discret

On recherche les probabilités p_i qui caractérisent la distribution. On note cette distribution f par abus. Un estimateur naturel est:

où n(x) est le nombre d'observations de l'échantillon qui sont égales à x. Une manière alternative de noter cet estimateur est:

où est la fonction indicatrice: elle vaut 1 lorsque son argument est vrai.

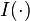
Le cas continu

L'estimateur précédent n'est plus valable, car dans le cas continu, on ne peut plus compter le nombre d'observations exactement égales à x. Par contre, on peut considérer une boîte centrée en x, et de largeur h, paramètre positif. On peut compter le nombre d'observations approximativement (et non plus exactement) égales à x, en comptant les observations tombant dans ladite boîte. L'estimateur devient:

où encore, en posant y_i = (x_i − x) / h:

.

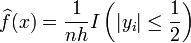
Le paramètre h contrôle le niveau de lissage de l'estimation et doit être recherché avec soin. L'estimateur précédent présente de bonnes propriétés comparables à celles d'une densité continue:

• il est positif ;
• il s'intègre à l'unité.

Toutefois, il présente un gros défaut pour pouvoir estimer une densité: il n'est pas continu. Pour gagner la continuité, on utilisera l'estimateur de Parzen (ou à noyau). Le principe est simple: il suffit de remplacer la fonction indicatrice par une fonction réelle, qui attribue un poids d'autant plus important que les observations sont situées à proximité de x.