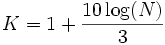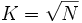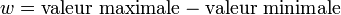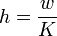Histogramme - Définition

Introduction

En statistiques, un histogramme est un graphe permettant de représenter la répartition d'une variable.

Un outil de gestion de la qualité

L’histogramme est un moyen rapide pour représenter la distribution d’un paramètre obtenu lors d’une fabrication.

Exemples :

• diamètre d’un arbre après usinage,
• dureté d’une série de pièces après un traitement thermique,
• concentration d’un élément dans la composition d’alliages produit par une fonderie,
• masse de préparation alimentaire dans une boîte de conserve,
• répartition de la luminosité des pixels dans une photographie.

L’histogramme est un outil « visuel » qui permet de détecter certaines anomalies ou de faire un diagnostic avant d’engager une démarche d’amélioration. Utilisé dans ce cadre, l’histogramme est un outil « qualitatif ». Pour pouvoir bien mener l’étude de la dispersion d’un paramètre à l’aide d’un ou de plusieurs histogrammes, il faut avoir une bonne connaissance du paramètre étudié. De même, il faut connaître les conditions de collecte des données : fréquence de mesure, outil de mesure utilisé, possibilité de mélange de lots, possibilité de tri etc.

Construction

Collecte des données

La première phase est la collecte des données en cours de fabrication. Cette collecte peut être réalisée soit de façon exceptionnelle à l’occasion de l’étude du paramètre soit en utilisant un relevé automatique ou manuel fait lors d’un contrôle réalisé dans le cadre de la surveillance du procédé de fabrication.

Sans qu’il soit réellement possible de donner un nombre minimum, il faut que le nombre de valeurs relevées soit suffisant. Plus on dispose d’un nombre élevé de valeurs, plus l’interprétation sera aisée.

Nombre de classes

La première opération est de déterminer le nombre de classes de l’histogramme. Généralement, dans le cadre d’une analyse de ce type, on utilise des classes de largeur identique.

Le nombre de classes dépend du nombre de valeurs N dont on dispose.

Le nombre de classes K peut être déterminé par la formule suivante :

ou plus simplement

Cependant, l’histogramme étant un outil visuel, il est possible de faire varier le nombre de classes. Ceci permet de voir l’histogramme avec un nombre différent de classes et ainsi de trouver le meilleur compromis qui facilitera l’interprétation. L’utilisation d’un logiciel dédié ou plus simplement d’un tableur facilite cette opération.

Intervalles de classe

L’amplitude w de l’histogramme est

L’amplitude h théorique de chaque classe est alors :

Il faut arrondir cette valeur à un multiple de résolution de l’instrument de mesure (arrondi à l'excès).

Exemple : Soit la masse d’une préparation culinaire avant conditionnement. Le calcul d'amplitude de classe donne h_th = 0,014 kg. La résolution de la balance utilisée est de 0,001 kg. On arrondit la valeur h à 0,015 kg.

Les classes peuvent être du type [limite _inférieure ; limite _supérieure[ ou ] limite _inférieure ; limite _supérieure].

La valeur minimale de la première classe est donnée par la valeur minimale de la série moins une demi-résolution.

Exemple : la valeur la plus petite relevée lors de la fabrication de la préparation culinaire est de 0,498 kg. La limite inférieur sera : 0,498 – (0,001 / 2) = 0,4975 kg.

Pour plus de facilité, il est préférable de prendre une valeurs « ronde » par exemple 0,495 kg

Exemple

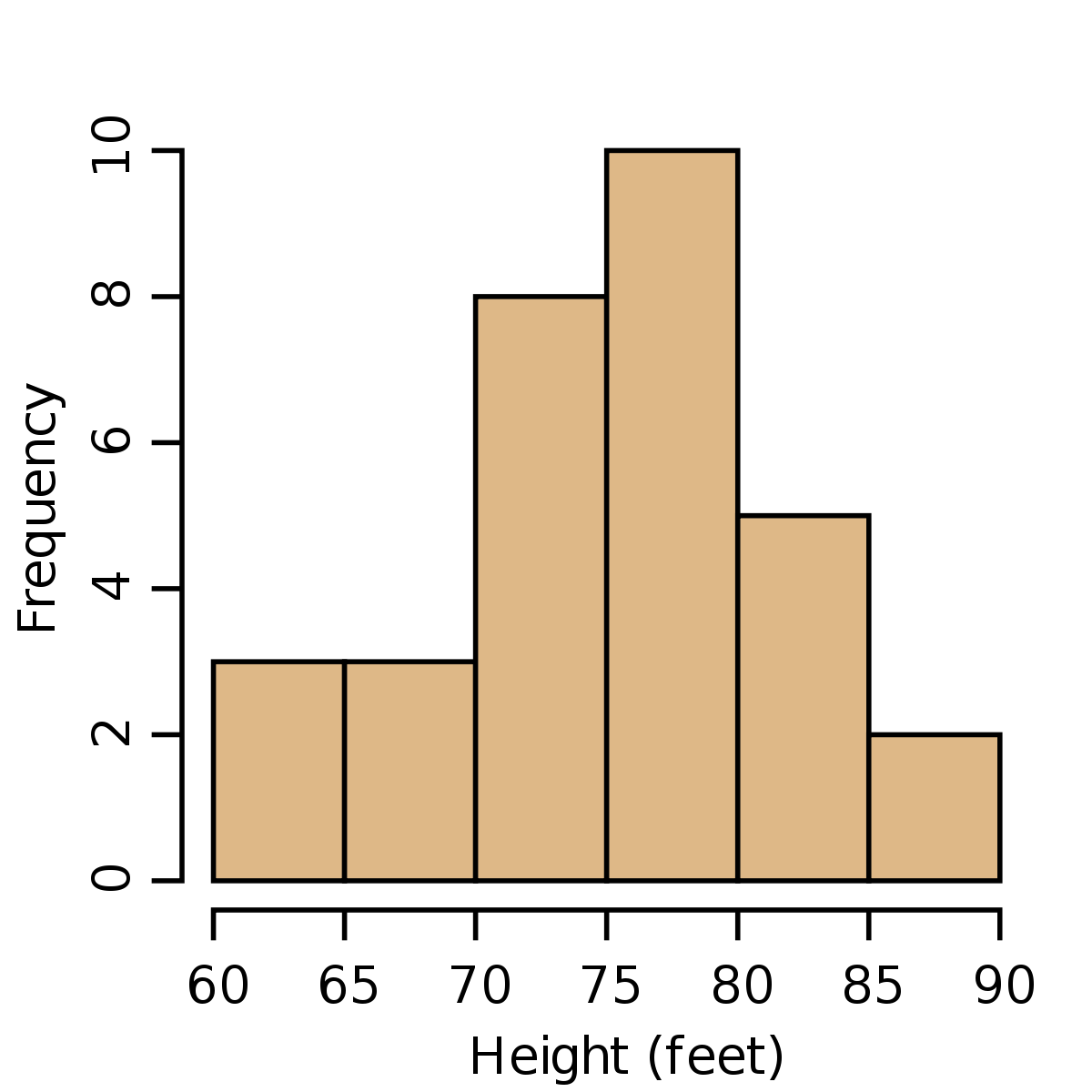
Soit la fabrication de rations alimentaires, la pesée des rations avant emballage donne la série de mesures suivantes en kg :

0,547	0,563	0,532	0,521	0,514	0,547	0,578	0,532	0,552	0,526	0,534	0,560	0,502	0,503	0,516	0,565
0,532	0,574	0,521	0,523	0,542	0,539	0,543	0,548	0,565	0,569	0,574	0,596	0,547	0,578	0,532	0,552
0,554	0,596	0,529	0,555	0,559	0,503	0,499	0,526	0,551	0,589	0,588	0,568	0,564	0,568	0,556	0,523
0,526	0,579	0,551	0,584	0,551	0,512	0,536	0,567	0,512	0,553	0,534	0,559	0,498	0,567	0,589	0,579

Les caractéristiques du relevé sont les suivantes :

• Le nombre d'échantillons : N=64
• L'étendue : w=0,098 kg
• Valeur minimale : 0,498 kg
• Valeur maximale : 0,596 kg

On en déduit les paramètres suivants pour l'histogramme :

• Le nombre de classes est de 7 (en utilisant la formule avec le logarithme)
• L'amplitude de classe est 0,098/7 = 0,014 kg que l'on arrondit à 0,015 kg (résolution de la balance : 0,001 kg)
• La valeur minimale de la première classe est de 0,498 – (0,001/2) = 0,4975. Par souci de facilité pour l'interprétation, on peut arrondir cette valeur à 0,495 kg.

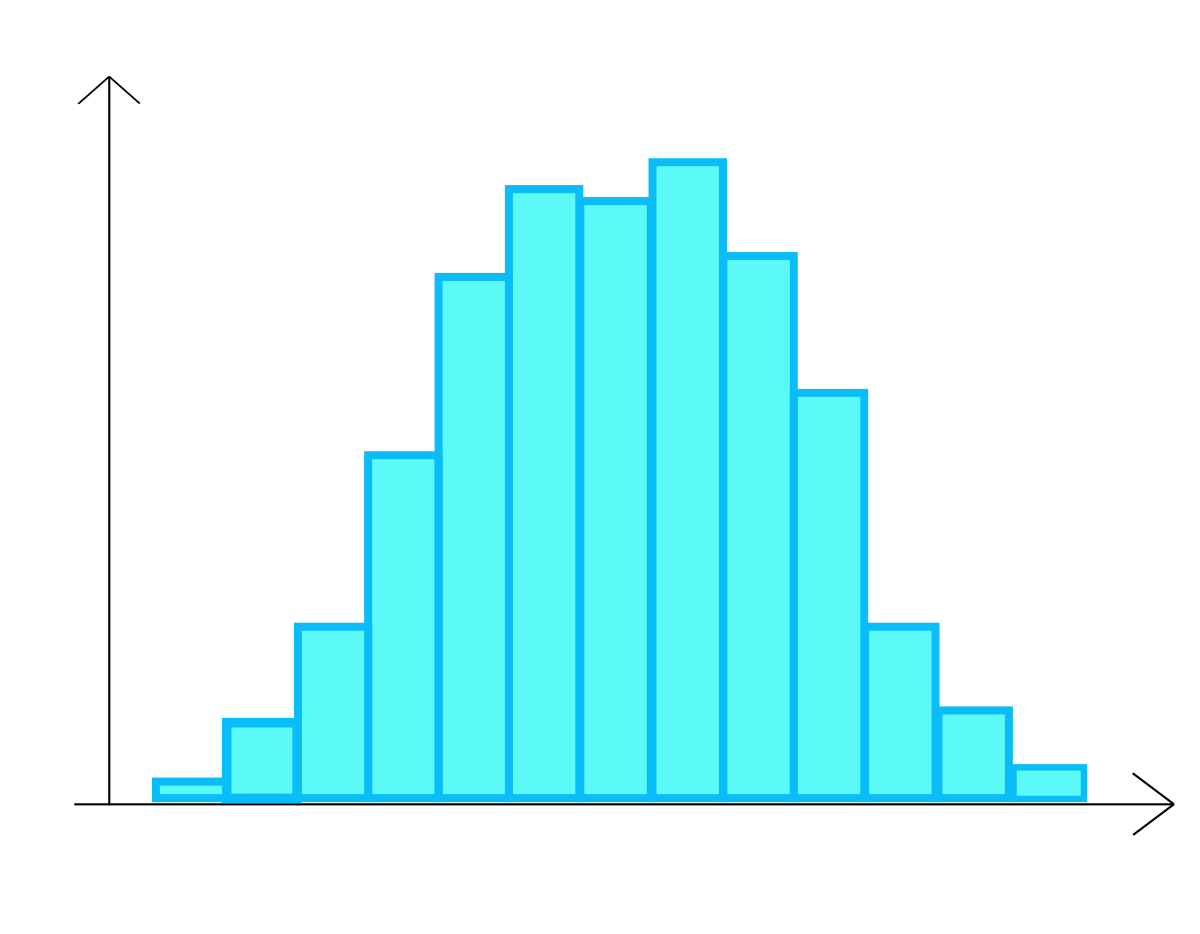
On obtient l'histogramme suivant :

Interprétation

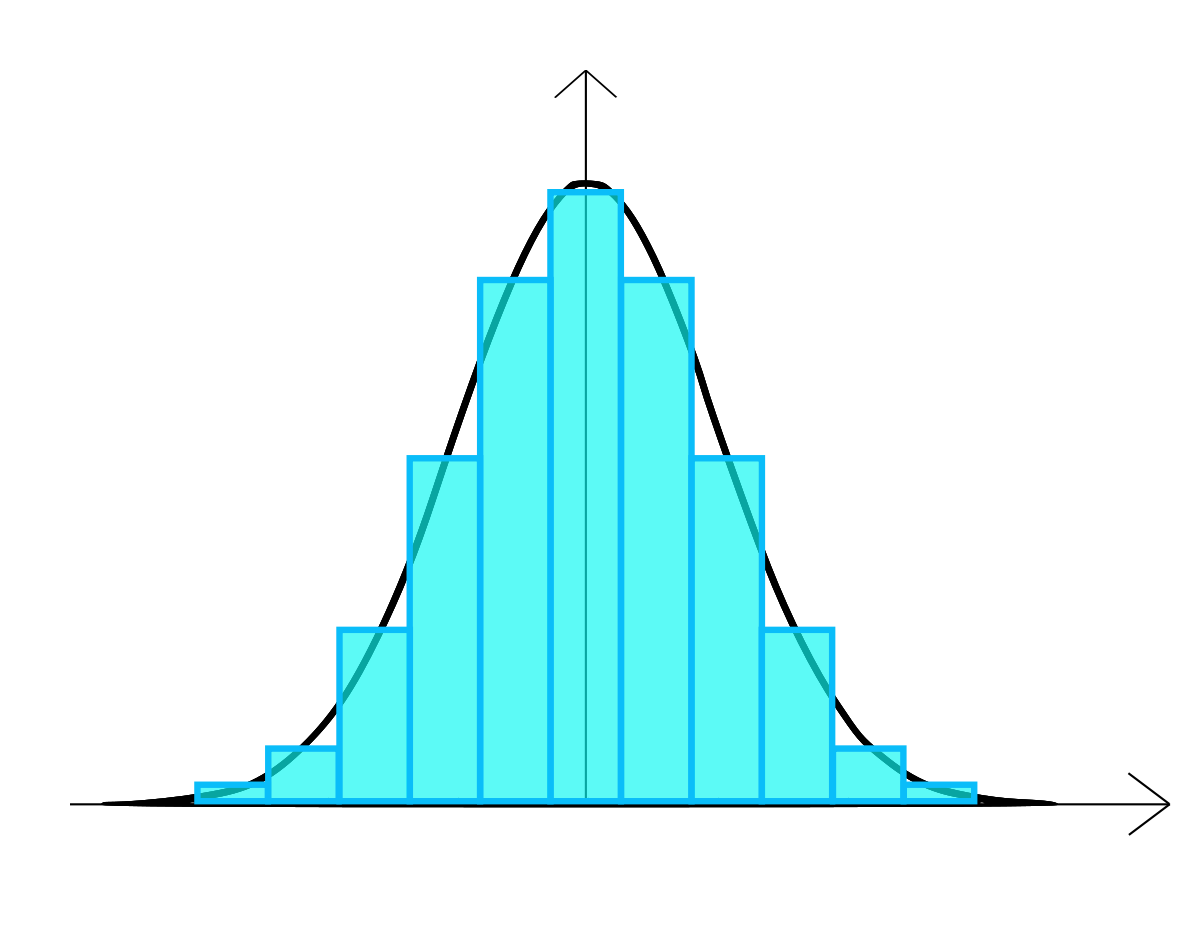
La distribution de beaucoup de paramètres industriels correspond souvent à une loi normale. On compare souvent l'histogramme obtenu au profil « en cloche » de la loi normale. Cette comparaison est visuelle et même si elle peut être une première approche, elle ne constitue pas un test de « normalité ». Pour cela, il faut exécuter un test dont un des plus classiques est la droite de Henry.

La distribution suivant la loi normale, si elle est extrêmement fréquente, n'est pas systématique. On vérifiera que la distribution ne correspond pas à une distribution de défaut de forme (exemple : mesure de l'excentration dans un tube, position d'objets lancés dans la direction d'un mur dont certains rebondissent sur ce mur).

L'interprétation peut, par exemple, donner les résultats suivants :

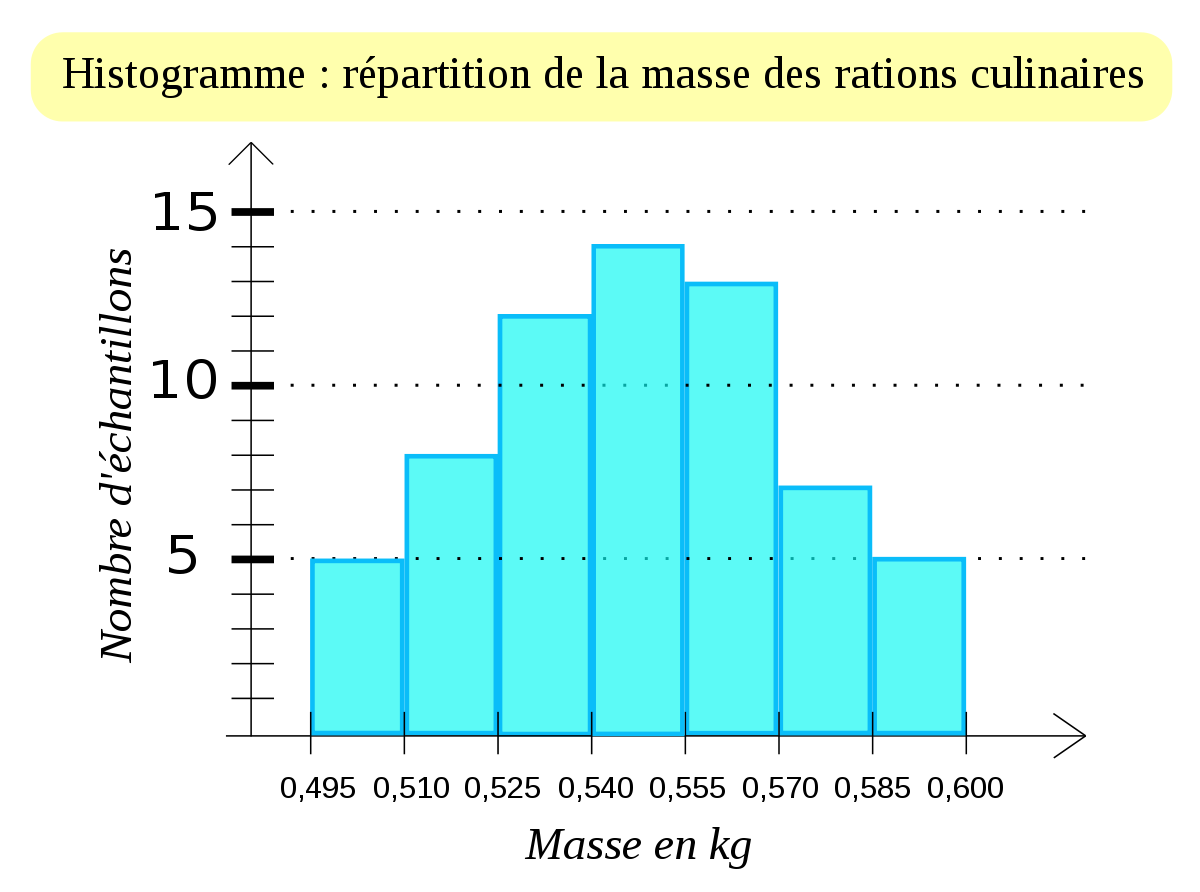
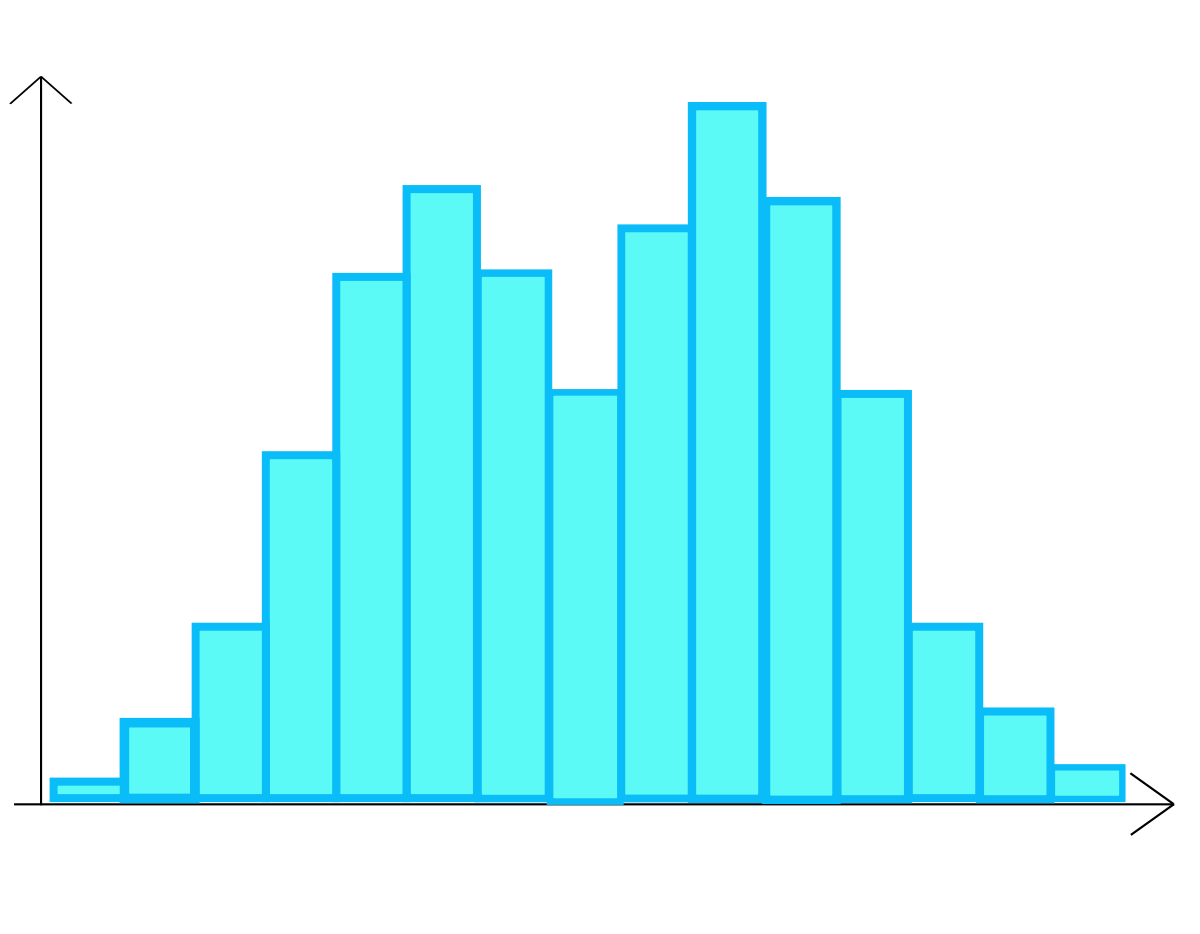
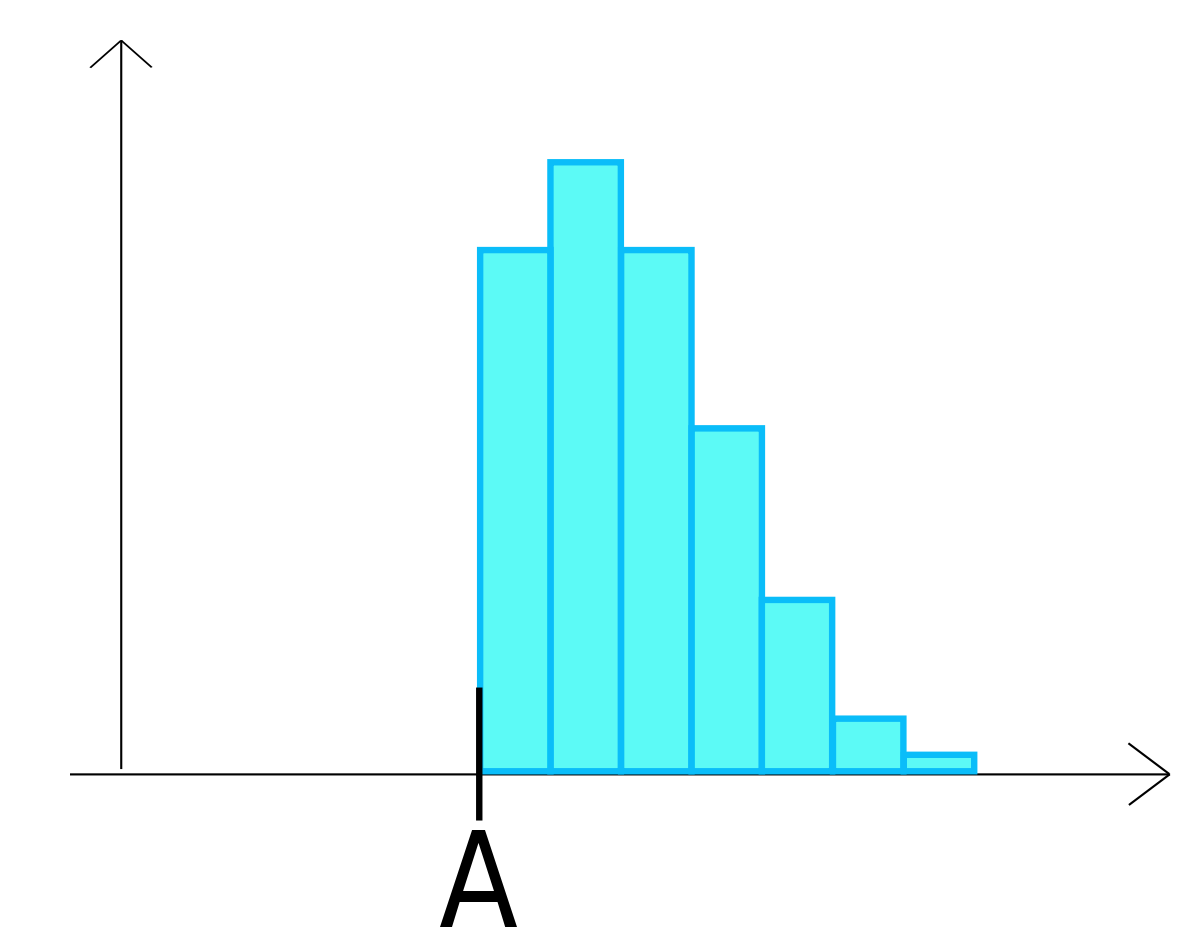
Histogramme montrant un mélange de deux lots.	Histogramme montrant un mélange de deux lots mais avec une moyenne proche. On veillera dans ce cas à faire aussi varier le nombre de classes pour vérifier qu'il ne s'agit pas d'un problème de construction.	Histogramme montrant que le lot a subi un tri. Tous les éléments pour lesquels la valeur du paramètre mesuré était inférieure à A ont été supprimés.

Dans le cas d'histogramme montrant un mélange de deux lots ayant une moyenne différente, il existe des cas où la dispersion présente cet aspect sans pour autant incriminer un mélange. C'est par exemple le cas de la mesure d'une pièce cylindrique mais qui présente un défaut de type ovalisation. Les deux moyennes représentent alors le grand diamètre et le petit diamètre. C'est la connaissance du procédé et/ou du produit qui permet de réaliser ce type d'interprétation.